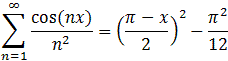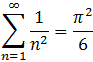8. Sequences of Functions
8.3. Series and Power Series
This section will combine two theories we discussed previously:
- sequences of functions that could converge pointwise or uniformly
- numeric series defined as a limit of a (numeric) sequence of partial sums
A simple example for a numeric series was the geometric series
.gif) . If a numeric series
converged, it represented a complicated way to express the resulting limit value.
For example, a complicated way to write the number 1 would be:
. If a numeric series
converged, it represented a complicated way to express the resulting limit value.
For example, a complicated way to write the number 1 would be:
1 = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... =.gif)
In this section we will replace the numeric summand by one that depends on x and try to analyze what happens.
| Definition 8.3.1: A Function Series | |
Suppose { fn(x) } is a sequence of functions and we
define the N-th partial sum as
SN(x) =Let D be the set of points for which the sequence of partial sums converges pointwise. Then, for x  D, we denote the
resulting limit function by D, we denote the
resulting limit function by
| |
It is clear that each SN, being a finite sum, is a well-defined function that inherits its properties from the fn's. But we would like to know when the infinite sum is well-defined and what can be said about its properties.
The above examples (with different degrees of difficulty) show that function series can result in simple functions that share properties with the individual terms fn(x) yet can be more complicated at the same time. For example, each term in the geometric function series is differentiable for all x yet when we add up infinitely many of these simple terms the resulting function is not even defined for |x| > 1.
We would like to develop a general theory of function series that will allow us to find properties of series quickly and efficiently. The basis of our discussion will be:
| Theorem 8.3.3: Weierstrass Convergence Theorem | |
Suppose fn are a sequence of functions defined on
D such that
where || fn ||D is the sup-norm on D. Then the (function) series  fn(x)
converges absolutely and uniformly on D to a function
f. If, in addition, each fn is continuous,
the limit function f is also continuous on D. fn(x)
converges absolutely and uniformly on D to a function
f. If, in addition, each fn is continuous,
the limit function f is also continuous on D.
| |
Weierstrass' theorem, if it applies, is nice because it lets you draw conclusions about a series of functions by looking at a numeric series of sup's. A simple example is the geometric series, writen as a series of monomials in x, each defined on a closed subset of (-1, 1):
| Example 8.3.4: Function Series Examples | |
| |
The above examples, especially the first, might seem somewhat special and perhaps a little contrived. After all, in the first example the terms of the series are so simple and add up (in the proof) so nicely that there might be reason to suspect an example ready-made for students. The other series, on the other hand, seem much more complicated than its constituent components. As it turns out, adding up a bunch of relatively simple functions, even monomials, can yield very complicated functions. Here it is definitely true:
The sum can be much more complicated than its parts!
The next theorem is going to be the cornerstone of a new theory that will even (finally and unexpectedly) provide a solid theoretical foundation for our trig functions sin and cos. Sic!
But, let's get started, as usual with a new definition:
| Definition 3.3.5: Power Series | |
A function series of the form
is called a (formal) power series centered at c. | |
In other words, a power series is an infinite series of functions where each term consists of a coefficient an and a power (x-c)n. Here are a few examples of power series:
| Example 3.3.6: Formal Power Series Examples | |
| |
The above definition of a power series is "formal" because the series may or may not converge. But power series, actually, have very nice and structured convergence properties:
| Theorem 3.3.7: Power Series | |
Every power series
 an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
an (x - c)n =
a0 +
a1(x-c) +
a0(x-c)2 + ...
centered at c has the following properties:
Note that it is possible for the radius of convergence to be zero (i.e. the power series converges only for x = c) or to be  (i.e. the series converges for all
x). Note that this theorem is sometimes called Abel's theorem on
Power Series. (i.e. the series converges for all
x). Note that this theorem is sometimes called Abel's theorem on
Power Series.
| |
A power series is, simply put, an "infinite polynomial", i.e. a polynomial of "infinite" degree:
- p(x) = 1 + 2x + 3x2 + 4x3 is a polynomial of degree 3
- q(x) = 1 + 2(x-1) + 3(x-1)2 is a polynomial of degree 2 centered at c = 1. Note that we could work out the parenthesis to obtain an equivalent polynomial centered at c = 0 (do it)
- f(x) = 1 + 2x + 3x2 + 4x3 + ... =
n xn-1 is a power series centered at c = 0 with some radius of convergence
- g(x) = 1 + 1/2(x+2) + 1/4(x+2)2 + 1/8(x+2)3 + ... =
1/2n (x+2)n is a power series centered at c = -2 with some radius of convergence
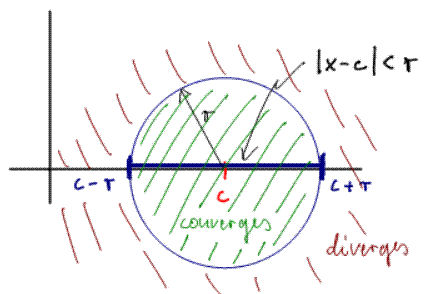
A power series converges when x = c because then all but the first term are zero. In addition, the series converges in the open interval c - r to c + r and diverges outside that interval, according to the theorem. The theorem makes no statement about convergence or divergene at the endpoints c - r and c + r, so these endpoints should be investigated 'manually'.
If you draw a circle centered at c with radius r then the circle intersects the x-axis at the points c - r and c + r and thus defines the regions of convergence and divergence. But it turns out that power series are best defined in the space of complex numbers, i.e. all coefficients and variables are allowed to be complex-valued. The Power Series theorem remains true in the complex plane and the set |z - c| < r would be a true circle inside which the (complex) series converges and diverges outside. On the boundary of the disk no general statement exists except for the fact that there must be at least one (possibly complex) point on the boundary where the series does not converge (otherwise you could increase the radius of convergence slightly).
Power series are studied extensively in Complex Analysis; in real analysis they are only a shadow of their true self ...
As a final note, the above theorem gives an explicit formula for the radius of convergence for a power series, which is nice. However, in most cases we could also apply our familiar Ratio Test we studied in chapter 4 to the terms of the series including the powers of x and to 'solve' for x. That way there is one less formula to memorize (assuming of course you remember the ratio test, which surely you do -:)!
For example, consider the power series
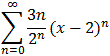 .
Clearly the series has c = 2 as center of convergence. To find
the radius of convergence, we could apply the above formula:
.
Clearly the series has c = 2 as center of convergence. To find
the radius of convergence, we could apply the above formula:
r = lim sup | an / an+1|
where an = 3n / 2n. We get:
r =
=
Thus, the radius of convergence is 2 and the series converges absolutely and uniformly on any subinterval of |x - 2| < 2.
To apply the ratio test to the same series, recall that the ratio test says that
 an
converges absolutely if
lim sup |an+1| / |an| < 1. Note that for
the ratio test the an+1 will be on top and will include
powers of x whereas in the formula for the radius of convergence
it shows up on the bottom and does not include any x's.
an
converges absolutely if
lim sup |an+1| / |an| < 1. Note that for
the ratio test the an+1 will be on top and will include
powers of x whereas in the formula for the radius of convergence
it shows up on the bottom and does not include any x's.
Let's now apply the ratio test to our series, but this time we let an = 3n / 2n (x-2)n. According to the ratio test our series converges absolutely if:
But that simplifies to the condition
As before, this means that the series converges if |x - 2| < 2, i.e. the radius of convergence is 2.
Either method has pros and cons:
- If you apply the formula for the radius of convergence directly, the terms seem a little simpler since you don't carry around any powers of x. On the other hand, you need to remember to put the term an on top, different from the well-known ratio test.
- If you apply the ratio test you do not need to remember any additional formula. But you need to carry around powers of x (which will, on the other hand always reduce nicely) and you must remember to solve the resulting inequality.
Regardless of the method we used to find the above radius of convergence r=2 we still need to check convergence at the endpoints x=0 and x=4. In this case it would turn out that the series diverges at both endpoints - make sure to verify that.
| Example 8.3.8: Power Series Examples | |
| |
Occasionally the center of a power series is more tricky to detect, or you might want to 're-center' a series (which does not always work). The following examples will let you gain some more experience with power series.
| Example 8.3.9: Power Series Center | |
| |
Of course polynomials are relatively simple functions: they can be added, subtracted, and multiplied (but not divided), and you again get a polynomial. Differentiation and integration are particularly simple and yield again polynomials. Lot's more is known about polynomials (e.g. they can have at most n zeros) and we feel pretty comfortable with them.
As it will turn out, power series share many of these properties, allowing us to think of them as "polynomial with infinite degree". Since we can add, subtract, and multiply absolutely convergent series (see chapter 4) we can add, subtract, and multiply (think Cauchy product) power series, as long as they have overlapping regions of convergence. Even differentiating and integrating works as it should:
| Theorem 8.3.10: Differentiating and Integrating Power Series | |
Let
 an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
an (x - c)n
be a power series centered at c with radius of convergence
r > 0. Then:
| |
The essence of this theorem, thinking of power series as infinite polynomials, is:
a0 + a1(x-c) + a2(x-c)2 + ... dx =
=a0 dx +
a1(x-c) dx +
a2(x-c)2 dx + ... =
= a0 (x-c) + 1/2 a1(x-c)2 + 1/3 a2(x-c)3 + ... + const
and for differentiation:
a0 + a1(x-c) + a2(x-c)2 + ... =
=a0 +
a1(x-c) +
a2(x-c)2 + ... =
= a1 + 2 a2(x-c) + 3 a3(x-c)2 + ...
Of course the derivative of a power series is again a power series with the same center and radius of convergence as the original series. Thus, a power series can be differentiated again, and again, and again, so that we have the following corrolary:
Corollary 8.3.11: Power Series is infinitely often Differentiable
| |
If a power series
f(x) = |  an (x-c)n
has radius of convergence r, then f is
infinitely often differentiable for |x-c| < r. In
other words,
f
an (x-c)n
has radius of convergence r, then f is
infinitely often differentiable for |x-c| < r. In
other words,
f  C
C (c-r, c+r)
. (c-r, c+r)
.
| |
The next examples let you experiment with differentiating and integrating power series. You will find that sometimes power series represent well-known "simple" functions, a theme we will pick up in detail in the next section.
| Example 8.3.12: Differentiating and Integrating Power Series | |
| |
| Example 8.3.13: A Series Approximation of Pi | |
| |
 Interactive Real Analysis
Interactive Real Analysis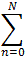 fn(x)
fn(x)
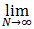 SN(x) =
SN(x) =
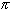 we have:
we have: 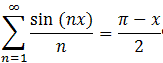
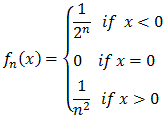 Does
Does 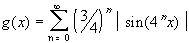 represents
a continuous function, called the
represents
a continuous function, called the
 p, where
p < r, and diverges for all |x - c| > r.
The number r is called the radius of convergence for the
power series and is given by:
p, where
p < r, and diverges for all |x - c| > r.
The number r is called the radius of convergence for the
power series and is given by:
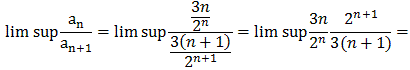
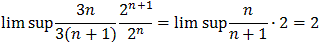
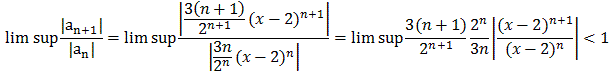
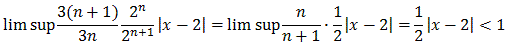
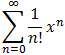 .
What is the radius of convergence? Make sure to simplify your answer, which
should be surprising. Can you use your result to figure out what function
this power series represents?
.
What is the radius of convergence? Make sure to simplify your answer, which
should be surprising. Can you use your result to figure out what function
this power series represents?
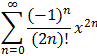 twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
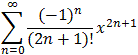 .
Simplify your answer and compare with the previous example. Can you use your
results to figure out what function this power series represents?
.
Simplify your answer and compare with the previous example. Can you use your
results to figure out what function this power series represents?