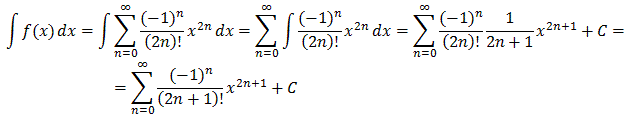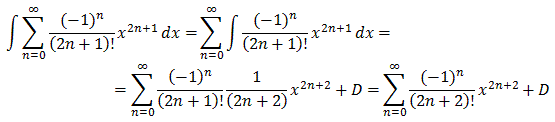8.3. Series and Power Series
Example 8.3.12 (b): Differentiating and Integrating Power Series
Integrate the series
f(x) = 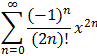 twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
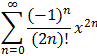 twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
twice and simplify your answer. Can you use your result to figure out what function
this power series represents?
The series converges for all x (confirm!) and can therefore be integrated (and differentiated) term-by-term. We have:
and integrating again:
Now, the above integration is technically correct, but with all the summation signs, integrals, and indeces it is difficult to see what is really going on. Things get a little clearer if we write out the series and integrate 'manually':
f(x) ==
= 1 - 1/2! x2 + 1/4! x4 - 1/6! x6 + ...
Integrating gives us a new function g(x):
g(x) =f(x) dx = x - 1/3! x3 + 1/5! x5 - 1/7! x7 + ... + C
Integrating again gives us:
g(x) dx = 1/2 x2 - 1/4! x4 + 1/6! x6 - 1/8! x8 + ... + Cx + D =
= -f(x) + 1 + Cx + D' =
= -f(x) + Cx + D''
where we subsume the +1 into the new constant D'.
In other words, if we ignore the constants we have two functions f and g such that
f(x) dx = g(x) and
g(x) dx = -f(x)
Hmmm ... what well-known functions could f and g be? To help your memory, here is the graph of these functions:
f(x) = 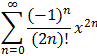
g(x) = 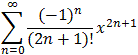
 Interactive Real Analysis
Interactive Real Analysis