8. Sequences of Functions
8.2. Uniform Convergence
We saw in the previous section that pointwise convergence of a sequence of functions was easy to define, but was too simplistic of a concept. We would prefer a type of convergence that preserves at least some of the shared properties of a function sequence. Such a concept is uniform convergence.
| Definition 8.2.1: Uniform Convergence | |
A sequence of functions { fn(x) } with domain
D converges uniformly to a function f(x) if given any
 > 0 there is a positive
integer N such that > 0 there is a positive
integer N such that
| fn(x) - f(x) | <
Please note that the above inequality must hold for all x
in the domain, and that the integer N depends only on
| |
We should compare uniform with pointwise convergence:
- For pointwise convergence we could first fix a value for x and then choose N. Consequently, N depends on both
and x.
- For uniform convergence fn(x) must be uniformly close to f(x) for all x in the domain. Thus N only depends on
but not on x.
Let's illustrate the difference between pointwise and uniform convergence graphically:
Pointwise Convergence Uniform Convergence For pointwise convergence we first fix a value x0. Then we choose an arbitrary neighborhood around f(x0), which corresponds to a vertical interval centered at f(x0).
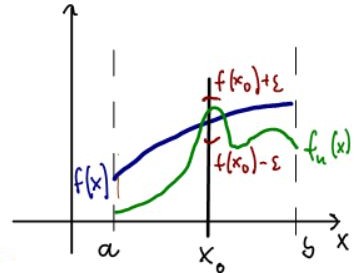
Finally we pick N so that fn(x0) intersects the vertical line x = x0 inside the interval (f(x0) -
, f(x0) +
)
For uniform convergence we draw an
-neighborhood around the entire limit function f, which results in an "
-strip" with f(x) in the middle.
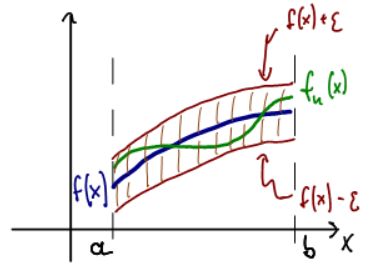
Now we pick N so that fn(x) is completely inside that strip for all x in the domain.
| Example 8.2.2: Pointwise versus Uniform Convergence | |
| |
Uniform convergence clearly implies pointwise convergence, but the converse is false as the above examples illustrate. Therefore uniform convergence is a more "difficult" concept. The good news is that uniform convergence preserves at least some properties of a sequence.
| Theorem 8.2.3: Uniform Convergence preserves Continuity | |
| If a sequence of functions fn(x) defined on D converges uniformly to a function f(x), and if each fn(x) is continuous on D, then the limit function f(x) is also continuous on D. | |
Before we continue, we will introduce a new concept that will somewhat simplify our discussion of uniform convergence, at least in terms of notation: we will use the supremum of a function to define a 'norm' of f.
| Definition 8.2.4: Supremum Norm | |
Suppose
f: D  R
is a function with domain D. We define the sup-norm of
f over D as: R
is a function with domain D. We define the sup-norm of
f over D as:
|| f ||D = sup{ |f(x)|: xIf the context is clear, we simply write || f ||. | |
Clearly, a function f is bounded if and only if
|| f || <  , which follows
immediately from the various definitions. The connection between sup-norm
and uniform convergence is also straight-forward.
, which follows
immediately from the various definitions. The connection between sup-norm
and uniform convergence is also straight-forward.
| Proposition 8.2.5: Sup-norm and Uniform Convergence | |
A sequence
fn: D  R
converges uniformly to
f: D R
converges uniformly to
f: D  R
if and only if R
if and only if
| |
Using this proposition it is can be easy to show uniform convergence of a function sequence, especially if the sequence is bounded. Still, even with this idea of sup-norm uniform convergence can not improve its properties: it preserves continuity but has a hard time with differentiability.
| Example 8.2.6: Uniform Convergence does not imply Differentiability | |
| |
So uniform continuity is good enough to preserve continuity, but does not preserve differentiability. Our next question will of course be: what is the impact on integration? We already know that pointwise convergence does not preserve Riemann-integrability, and even if it does we can not switch limits and integration. What about uniform convergence?
| Theorem 8.2.7: Uniform Convergence and Integration | |
Let fn(x) be a sequence of continuous functions
defined on the interval [a, b] and assume that
fn converges uniformly to a function f.
Then f is Riemann-integrable and
| |
Note: Much more can be said about convergence and integration if we consider the Lebesgue integral instead of the Riemann integral. To focus on Lebesgue integration, for example, we would first define the concept of "convergence almost everywhere":
| Definition 8.2.8: Convergence Almost Everywhere | |
| A sequence fn defined on a set D converges (pointwise or uniformly) almost everywhere if there is a set S with Lebesque measure zero such that fn converges (pointwise or uniformly) on D \ S. We say that fn converges (pointwise or uniformly) to f a.e. | |
In other words, convergence a.e. means that a sequence converges everywhere except on a set with measure zero. Since the Lebesgue integral ignores sets of measure zero, convergence a.e. is ready-made for that type of integration.
| Example 8.2.9: Convergence Almost Everywhere | |
|
Let rn be the (countable) set of rational numbers inside the interval [0, 1], ordered in some way, and define the functions
| |
There are many theorems relating convergence almost everywhere to the theory of Lebesgue integration. They are too involved to prove at our level but they would certainly be on the agenda in a graduate course on Real Analysis. For us we will be content stating, without proof, one of the major theorems: the Lebesgue bounded convergence theorem.
| Theorem 8.2.10: Lebesgue's Bounded Convergence Theorem | |
Let { fn } be a sequence of (Lebesgue) integrable
functions that converges almost everywhere to a measurable function
f. If
|fn(x)|  g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and: g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and:
| |
It remains to clarify the connection between uniform convergence and differentiability. Simple - or pointwise - convergence is not enough to preserve differentiability, and neither is uniform convergence by itself. However, if we combine pointwise with uniform convergence we can indeed preserve differentiability and also switch the limit process with the process of differentiation.
| Theorem 8.2.11: Uniform Continuity and Differentiation | |
Let fn(x) be continuously differentiable functions
defined on the interval [a, b]. If:
Then f is differentiable and f'(x) =for all x  [a, b]. In other
words, the limit process and the differentiation process can be switched in
this case. [a, b]. In other
words, the limit process and the differentiation process can be switched in
this case.
| |
One of the main applications of our theory of uniform convergence is going to be series of functions and in particular power series ... which we will cover next.
 Interactive Real Analysis
Interactive Real Analysis N
N
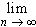 ||fn - f||D = 0
||fn - f||D = 0
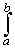 fn(x) dx
=
fn(x) dx
=
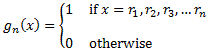 and
and
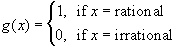
 | fn - f | dm = 0
| fn - f | dm = 0