8.2. Uniform Convergence
Theorem 8.2.10: Lebesgue's Bounded Convergence Theorem
Let { fn } be a sequence of (Lebesgue) integrable
functions that converges almost everywhere to a measurable function
f. If
|fn(x)|  g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and:
g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and:
Please refer to any standard Graduate-level textbook on Analysis for
the - involved - proof.
 g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and:
g(x)
almost everywhere and g is (Lebesgue) integrable, then
f is also (Lebesgue) integrable and:
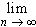
| fn - f | dm = 0
 Interactive Real Analysis
Interactive Real Analysis