8.3. Series and Power Series
Example 8.3.8 (b): Power Series?
Is the series
f(x) = 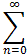 32nxn
a power series? If so, list center, radius of convergence, and general term
an.
32nxn
a power series? If so, list center, radius of convergence, and general term
an.
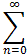 32nxn
a power series? If so, list center, radius of convergence, and general term
an.
32nxn
a power series? If so, list center, radius of convergence, and general term
an.
Yes, this is also a power series centered at c = 0. The general term here is
an = 32n = (32)n = 9n
According to our formula the radius of convergence is:
r = lim sup | an / an+1 | = lim sup | 9n / 9n+1 | = 1/9
Thus the series converges for |x| < 1/9. To determine exactly where the series converges we should check the endpoints of this interval manually:
- For x=-1/9:
32nxn =
9n(-1/9)n =
(-1)n, which diverges.
- For x=1/9:
32nxn =
9n(1/9)n =
1n, which diverges as well.
32nxn
f(x) = 1/1-9x
 Interactive Real Analysis
Interactive Real Analysis