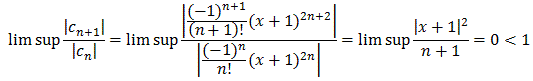8.3. Series and Power Series
Example 8.3.8 (d): Power Series?
Is the series
f(x) =  (-1)n/n! (x + 1)2n
a power series? If so, what is the center and radius of convergence?
List the first five coefficients a0, a1,
a2, a3, a4.
(-1)n/n! (x + 1)2n
a power series? If so, what is the center and radius of convergence?
List the first five coefficients a0, a1,
a2, a3, a4.
 (-1)n/n! (x + 1)2n
a power series? If so, what is the center and radius of convergence?
List the first five coefficients a0, a1,
a2, a3, a4.
(-1)n/n! (x + 1)2n
a power series? If so, what is the center and radius of convergence?
List the first five coefficients a0, a1,
a2, a3, a4.
If we write out the series we see it is indeed a power series with center c=-1 and all odd coefficients equal to zero:
f(x) = 1 - 1/1!(x+1)2 + 1/2! (x+1)4 - 1/3! (x+1)6 + ...
In particular:
- a0 = 1/0! = 1
- a1 = 0
- a2 = 1/1! = 1
- a3 = 0
- a4 = 1/2! = 1/2
To find the radius of convergence we could apply our usual formula, but it is a little confusing since every other an is zero. Thus, we go the alternate route, as discussed in the text, to simply apply the ratio test to the series. In other words, the series converges for those x for which:
But that means it converges for all x, or in other words
the radius of convergence r =  .
.
Incidentally, this series also has a simpler expression, as you can see from the plots below. After finishing the chapter, make sure to return here to figure out which function this series represents.
(-1)n/n! (x + 1)2n
f(x) = mystery
 Interactive Real Analysis
Interactive Real Analysis