8.3. Series and Power Series
Example 8.3.12 (d): Differentiating and Integrating Power Series
Find, with proof, a power series centered at c = 0 for the function
f(x) = 1/(1-x)2, for
-1 < x < 1.
We need to resort to information we already know. We did discuss the geometric series:
1/1-x =xn
Differentiating both sides finishes the problem:
f(x) = 1/(1-x)2 =1/1-x =
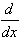
xn =
nxn-1
n xn-1
f(x) = 1/(1-x)2
 Interactive Real Analysis
Interactive Real Analysis