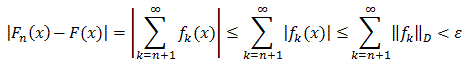Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 8.1. Pointwise Convergence
• 8.2. Uniform Convergence
• 8.3. Series and Power Series
• 8.4. Taylor Series
• 8.5. Approximation Theory
• 9. Historical Tidbits
• Java Tools

8.3. Series and Power Series

Theorem 8.3.3: Weierstrass Convergence Theorem

Suppose f_n are a sequence of functions defined on D such that

|| f_n ||_D <

where || f_n ||_D is the sup-norm on D. Then the (function) series f_n(x) converges absolutely and uniformly on D to a function f. If, in addition, each f_n is continuous, the limit function f is also continuous on D.

Context

The proof will involve two steps:

1. we will show that the series converges pointwise to a limit function F
2. the convergence to F is actually uniform

Let's get started with the first step. Fix x D. Then the series f(x) is a numeric series. In fact, since |f(x)| || f ||_D that numeric series must converge according to the Comparison Test to a limit L. That limit depends on x so that we can a function

F(x) = f(x)

which is well-defined (pointwise) for all x D.

Next we need to show that the convergence is uniform. Take any > 0. Since the numeric series || f_n ||_D converges we can find an integer N such that

< for all n > N

But then:

which means that the sequence of partial sums converges uniformly.

If we knew what uniformly Cauchy meant, we could also show that the sequence of partial sums was uniformly Cauchy, which (we would hope) should imply uniform convergence. To practice, define uniformly Cauchy sequences and finish the proof that way.

If, in addition, each f_n is continuous, then every N-partial sum is also continuous. Since uniform convergence preserves continuity, the limit would also be continuous.