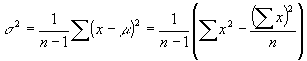4.4 Measures of Variability: Range, Variance, and Standard Deviation
While mean and median tell you about the center of your observations, it says nothing about the 'spread' of the numbers.
Example: Suppose two machines produce nails which are on average 10 inches long. A sample of 11 nails is selected from each machine.
- Machine A: 6, 8, 8, 10, 10, 10, 10, 10, 12, 12, 14
- Machine B: 6, 6, 6, 8, 8, 10, 12, 12, 14, 14, 14
To verify, let's compute the mean:
- mean for machine A: 110 / 11 = 10
- mean for machine B: 110 / 11 = 10
In both cases, the mean is 10, indeed. However, the first machine seems to be the better one, since most nails are close to 10 inches. Therefore:
We must find additional numbers indicating the 'spread' of the data.
The Range
The easiest measure of the data spread is the range. It is simply the highest data value minus the lowest data value (we have seen the range before). In the above example, the range is the same for both data, namely 14 - 6 = 8. The range is, while useful, too crude a measure of variability.
The Variance
We want to find out how much the data points are spread around the mean. To do that, we could find the difference between each data point and the mean, and average these differences. However, we want to measure the differences to the mean regardless of the sign (positive or negative difference). Therefore, we could find the absolute value of the difference between each data point and average that. But for theoretical reasons an absolute value function is not easy to deal with, so that one chooses a square function instead (which also neutralizes signs). Finally, for yet other theoretical reasons we shall use not the sample size n to compute an average, but instead n-1.
Hence, we will use this formula to compute the data spread, or variance:
Variance = add up the squares of (Data points - mean), then divide that sum by (n - 1)
There are two symbols for the variance, just as for the mean:
-
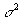 is
the variance for a population
is
the variance for a population -
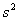 is
the variance for a sample
is
the variance for a sample
In other words, the variance is computed according to the formulas:
-
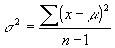 (for
the population variance)
(for
the population variance) -
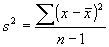 (for
the sample variance)
(for
the sample variance)
We had to use two formulas because one involves the population mean, the other the sample mean. Practically, however, the formula is the same. It is useful to compute the variance at least once "by hand" before we show how to use Excel to accomplish the same feat quickly and easily.
How to find the variance "by hand":
- Make a table of all x values
- Find the mean of the data
- Include a column with the difference to the mean
- Include a column with the square of difference to the mean
- Add the last column and divide the sum by (n - 1).
Here is the table that this procedure produces for the above sample of nails from machine A and B:
Machine A:
x 6 4 16 8 2 4 8 2 4 10 0 0 10 0 0 10 0 0 10 0 0 10 0 0 12 -2 4 12 -2 4 14 4 16
Therefore, the variance for machine A is: (16 + 4 + 4 + 0 + 0 + 0 + 0 + 0 + 4 + 4 + 16) / 10 = 48 / 10 = 4.8
Machine B:
x 6 4 16 6 4 16 6 4 16 8 2 4 8 2 4 10 0 0 12 -2 4 12 -2 4 14 -4 16 14 -4 16 14 -4 16
Therefore, the variance for machine B is: (16 + 16 + 16 + 4 + 4 + 0 + 4 + 4 + 16 + 16 + 16) / 10 = 112 / 10 = 11.2
In other words, the variance, or spread around the mean, for machine A is 4.8 while machine B has a variance (spread) of 11.2. That means that machine A, as a rule, produces nails that stick pretty close to the average nail length. Machine B, on the other hand, produces nails with more variability that machine A. Therefore, Machine A would be much preferred over machine B.
Note: The unit of the variance is the square of the original unit; hence, it is not the best number (considering units). Therefore, one introduces an additional number, called the standard deviation:
The Standard Deviation
The standard deviation is the square root of the variance.
As with the mean, there are two letters for variance and standard deviation:
-
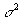 is
the variance for a population and
is
the variance for a population and
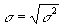 is
the population standard deviation
is
the population standard deviation -
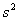 is
the variance for a sample and
is
the variance for a sample and
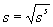 is
the sample standard deviation
is
the sample standard deviation
Example: Consider the sample data 6, 7, 5, 3, 4. Compute the standard deviation for that data.
To compute the standard deviation, we must first compute the mean, then the variance, and finally we can take the square root to obtain the standard deviation. In this case we do not need to create a table since there are so few numbers:
- Computing the mean:
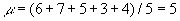
- Computing the variance:
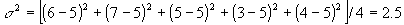
- Standard deviation:
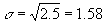
Short-Cut for Variance
There is a nice short-cut to compute the variance that can be proved as an exercise:
At first this second formula looks much more complicated, but it is actually easier since it does not involve computing the mean first. In other words, using the second formula we can compute the variance (and therefore the standard deviation) without first having to compute the mean.
In our above example of machine B we would compute the variance using this shortcut as follows:
x x2 6 36 6 36 6 36 8 64 8 64 10 100 12 144 12 144 14 196 14 196 14 196 sum(x) = 110 sum(x2) = 1212
Therefore the variance is:
1/ (11 - 1) * (1212 - 1102/11) = 0.1 * (1212 - 1100) = 11.2
which of course is the same number as before, but a little easier to arrive at. However, Excel - as usual - provides built-in function to compute the range, the variance, and the standard deviation.
If you need to compute the variance manually, you should always use this shortcut formula.
Using Excel to compute Range, Variance, and Standard Deviation
Excel provides simple formulas to compute the range, the variance, and the standard deviation:
- to compute the range: "=max(RANGE) - min(RANGE)"
- to compute the variance: "=var(RANGE)"
- to compute the standard deviation: "=stdev(RANGE)"
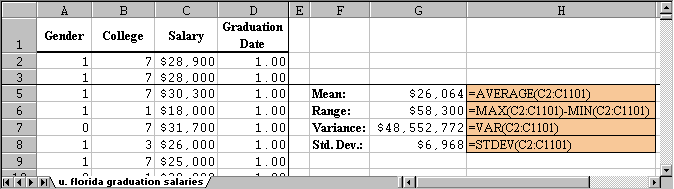
Example: Use the above formulas to compute the mean, the
range, the variance, and the standard deviation of the salaries of
graduates for the University of Florida. The data set (in Excel
format) can be obtained by using the
![]() University
of Florida Salary Levels data set we utilized beore.
University
of Florida Salary Levels data set we utilized beore.
All that is involved here is adding the appropriate formulas to the Excel worksheet. The results (including the formulas) are displayed below:
Note: The variance is displayed as dollars, even though that is not correct. The correct unit for the variance, of course, is "square dollars" which does not make much sense. The standard deviation, on the other hand, has indeed dollars as unit.
Variance and Standard Deviation for Frequency Tables
Just as we were able to approximate the mean and median of a variable from its distribution (frequency table or histogram) we can do something similar for the variance (and hence the standard deviation).
Example: A study of salaries of graduates from a University shows their income as follows:
Salary Range Count $7,200 - $18,860 130 $18,860 - $30,520 698 $30,520 - $42,180 254 $42,180 - $53,840 16 $53,840 - $65,500 2
Estimate the standard deviation for this variable. Hint: you may use the following table (of course together with Excel) to get organized. If you have trouble understanding this table, check the video below, explaining a slightly easier example.
Salary Range count mid count*mid mid2 cont*mid2 $7,200 - $18,860 130 13,030 1,693,900 169,780,900 22,071,517,000 $18,860 - $30,520 698 24,690 17,233,620 609,596,100 425,498,077,800 $30,520 - $42,180 254 36,350 9,232,900 1,321,322,500 335,615,915,000 $42,180 - $53,840 16 48,010 768,160 2,304,960,100 3,687,841,600 $53,840 - $65,500 2 59,670 119,340 3,560,508,900 7,121,017,800 Total 1,100 29,047,920 793,994,369,200
To estimate the variance we use the shortcut formula:
1/(n-1)*(sum of squares - (sum)2/N) =
= 1/1099*(793994369200 - 290479202/1100 =
= 1/1099 * 60111656176 = 54696684.42
Thus, the variance is approximately 54,696,684.42 and thus the standard deviation is the square root of that number, or $7,395.72. That is close enough to the true values computed previously.
The numbers in this example turned out to be huge, which made the process somewhat confusing. For smaller numbers, everything seems a little bit easier, hopefully.
Example: The evaluation of a statistics lecture resulted in the following frequency distribution. Find the mean, median, variance, and standard deviation.
Category Count very good 10 good 5 neutral 4 poor 2 very poor 1
Here we have a categorical variable whose mean, std dev. , etc. we want to compute. At first glance that won't work, since we can only compute those parameters for numeric variables. But since the variable is ordinal, it does make some sense to use numeric values as codes for the various categories and thus change the variable to a numeric one. Let's call it x. We (arbitrarily) decide on the codes:
very good: x = 5, good: x = 4, neutral: x = 3, poor: x = 2, very poor: x = 1Let's tackle the hardest parameter to compute first: the variance. We create the table we need to compute the variance (and the mean). It includes columns for the values of x and x2, as well as the products x*count and x2*count and their sums:
Category count x x*Count x2 x2*count very good 10 5 50 25 250 good 5 4 20 16 80 neutral 4 3 12 9 36 poor 2 2 4 4 8 very poor 1 1 1 1 1 sum 22 87 375
Now the hard work is done, so we can estimate the variance using the shortcut formula:
1/(n-1)*(sum of squares - (sum)2/N) =
= 1/21*(375 - 872/22) =
= 1/21* 30.954 = 1.474
The rest is easy:
std dev = sqrt(Variance) = sqrt(1.474) = 1.214
mean = 87/22 = 3.954
For the median, we will stick to the categories, not the codes, and use the cummulative percent of the frequency table. We leave the details to the reader (that's you ... yup, you! Wake up!) but the answer is:
median category: (x=4) or good"Fun" Facts: We mentioned that the above codes were arbitrary. What happens it we used different codes? Say, for example:
very good: x = 1, good: x = 2, neutral: x = 3, poor: x = 4, very poor: x = 5Verify that with these codes the mean turns out to be 2.045, but the variance comes out the same! Is that coincidence or is that always the case?
Choose a code that is 2*orginal code. In other words, choose
very good: x = 10, good: x = 8, neutral: x = 6, poor: x = 4, very poor: x = 2What is the mean and variance now? Can you find a rule for how the means are related for the two different codes?
Finally, while the codes are in principle arbitrary, in most cases it is best to use a linear code.
Finally (this time for real), if you don't want to memorize how to find mean and variance from a frequency table, you could reconstruct the original data from the table and find mean and variance the normal way (including using Excel or StatsCrunch). For example, say we want to find the mean and variance for a variable whose frequency distribution is as follows:
Category Count very good 8 good 5 neutral 7 poor 2 very poor 3
Using the (linear) code Very good = 1, good = 2, neutral = 3, poor = 4, very poor = 5, the frequency table implies that the data consists of 8 1's, 5 2's, 7 3's, 2 4's and 3 5's. In other words, the actual data is:
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 5, 5, 5
But now we can use Excel or StatCrunch to work out the mean and standard deviation real quick! Do it! This process becomes more tedious for large numbers of data points. For 1,000's of points (or more), it would be better to follow the procedure using the frequendcy table.
 MathCS.org - Statistics
MathCS.org - Statistics