MathCS.org - Statistics

back | next

4.5 Quartiles and Percentiles

At this point we can describe the results of an experiment using 2 numbers (or parameters): the mean (or median) and the standard deviation (computed from the variance). That will tell us the "center" of the distribution of values (mean) and the "spread" around that center (standard deviation). For example, if we measure the  height of US army soldiers we could say that the average height of US soldiers is 1.73 meters, with a standard deviation of 0.15 meters (the numbers are made-up). This gives you a reasonable idea about how a generic solder looks like (he/she is about 1.73 m tall) and how much variation from that generic look there is. To describe the distribution in more detail we need additional descriptive measures.

Upper and Lower Quartiles

Following this notation, the median should actually be called the "middle quartile" Q2, since it is that number such that 50% are less than it and 50% are larger.

NOTE: To find the quartiles, you must first sort your data (similar to finding the mean).

Example: Compute the upper and lower quartiles of the numbers 1, 2, 3, 4, 5, 6, 7.

The numbers are already sorted, so that it is easy to see that the median is 4 (three numbers are less than 4 and three are bigger). In other words, 4 splits our numbers up into the set of smaller numbers {1, 2, 3} and the set of larger ones {5, 6, 7}. The quartiles, in turn, split up these sets in the middle, so that Q1 = 2 and Q3 = 6.

Note that the numbers 1, 2 are less than or equal to the lower quartile, while 2, 3, 4, 5, 6, 7 are larger than or equal to Q1. Therefore, 2 out of 7 or 28% of values are less than or equal to Q1 and 6 out of 7 = 86% are larger than Q1.

Example: Compute the upper and lower quartiles of the numbers 1, 2, 3, 4, 5.

Now the median is 3, leaving two sets {1, 2} and {4, 5}. To split these numbers in the middle does not work, so it is not immediately clear what the quartiles are.

Similarly, the upper quartile can be shown to be 4.

For larger data sets, the quartiles can be selected as follows:

For Lower Quartile:
 
  • Sort all observations in ascending order
  • Compute the position L1 = 0.25 * N, where N is the total number of observations.
  • If L1 is a whole number, the lower quartile is midway between the L1-th value and the next one.
  • If L1 is not a whole number, change it by rounding up to the nearest integer. The value at that position is the lower quartile.
 For Upper Quartile:
 
  • Sort all observations in ascending order
  • Compute the position L3 = 0.75 * N, where N is the total number of observations.
  • If L3 is a whole number, the lower quartile is midway between the L3-th value and the next one.
  • If L3 is not a whole number, change it by rounding up to the nearest integer. The value at that position is the lower quartile.

Examples: Find the quartiles for the values 1, 2, 3, 4, 5, 6, 7 and also for the values 1, 2, 3, 4, 5 using this new method.

For the set 1, 2, 3, 4, 5, 6, 7 we have N = 7. Thus:

For the set 1, 2, 3, 4, 5 we have N = 5. Thus:

Percentiles

Quartiles are useful and they help to describe the distribution of values as we will see later. However, we often want to know how one particular data value compares to the rest of the data. For example, when taking standardized test scores such as SAT scores, I want to know not only my own score, but also how my score ranks in relation to all scores. Percentiles are perfect for this situation.

The k-th Percentile is that number such that K % of all data values are less and (100 - K) % are larger than it. More precisely, at least K% of the sorted values are less than or equal to it and at least (100 - K)% of the values are greater than or equal to it.

Note: The lower quartile is the same as the 25th percentile, the median is the same as the 50th percentile, and the upper quartile is the same as the 75th percentile.

To find the k-th Percentile:

Example: Consider the following cotinine levels of 40 smokers:

0 87 173 253 1 103 173 265 1 112
198 266 3 121 208 277 17 123 210 284
32 130 222 289 35 131 227 290 44 149
234 313 48 164 245 477 86 167 250 491

Find the quartiles and the 40th percentile.

First note that before we start our computations we must sort the data - computing percentiles for non-sorted data is the most common mistake (so please avoid it). Here is the same data again, this time sorted:

0 1 1 3 17 32 35 44 48 86
87 103 112 121 123 130 131 149 164 167
173 173 198 208 210 222 227 234 245 250
253 265 266 277 284 289 290 313 477 491

Now we can do our calculations, where N = 40 (number of values in our data set).

However, for percentiles another question is usually asked: given a particular value, find that percentile that corresponds to this value. In other words, determine how many values are less and how many values are larger than the particular value.

To find the percentile that corresponds to a particular data value x is:

  • percentile value of x = (number of values less than x) / (total number of values) * 100

Example: Suppose you took part in the above study of cotinine levels, and your personal continine level was 245. What is the percentile value of 245, and how many people in the study had a higher cotinine level that you?

First note that in our sorted data the value 245 is in 29th position (I used the sorted data, of course). Therefore, according to our formula:

Thus, by definition of percentiles, 72.5% of values are less than 245 while (100 - 72.5) = 27.5% are larger than 245.

Using Excel to find Percentiles

Of course Excel can be used to find percentiles, and therefore upper and lower quartiles (which are just the 25th and 75th percentile, respectively).

The Excel function to compute percentiles is "=percentile(RANGE, K)", where RANGE is a range of cells and K is the percentile to compute as a decimal number between 0 and 1. The data does not have to be sorted, Excel can handle it automatically.

The Excel function to compute the rank of a value x in a data set as a percentage of the data set (in other words, the percentile value of x) is "=percentrank(RANGE, X)". The data does not have to be sorted, Excel can handle it automatically.

For example, the function "=percentile(A1:A10, 0.4)" computes the 40th percentile of the values in the cells A1 to A10, while "=percentrank(A1:A10, 0.4)" computes the how many-th percentile the value of x is in the dataset.

Example: The following Excel spreadsheet contains some data about life expectancy and literacy rates in about 100 countries of the world in 1995. Compute the mean, median, variance, standard deviation, and upper and lower quartile of the life expectancy and percentage of people who read. What is the percentile value for life expectancy in Japan, the USA, and in Afghanistan?

Life Expectancy Data

We use the formulas "average", "median", "var", and "stdev" as introduced previously to compute the various descriptive statistics. The new formula "percentile" is used to computer the quartiles as well as the 40th percentile. Note that the data does not have to be sorted when using these formulas, Excel will take care of that problem automatically.

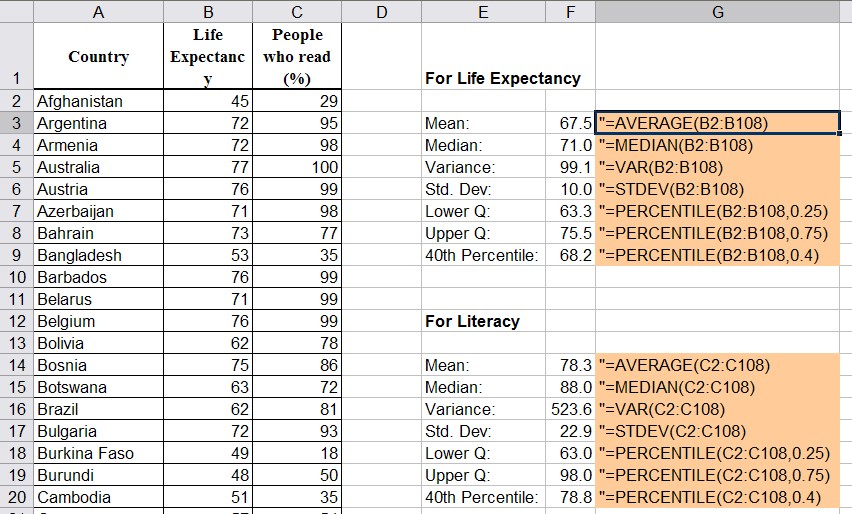
To find the relative ranking (aka percentiles) for Japan, the USA, and Afghanistan we use the "percentrank" function where we substitute the life expectancy for the respective countries for x:

Since these numbers are in percent, we have:

Example: To practice, use the previous life expectancy data and compute the mean, mode, median, variance, and standard deviation, the max and min values, and the upper and lower percentages.