7.4. Lebesgue Integral
Why these ads ...
We previously defined the Riemann integral roughly as follows:
- subdivide the domain of the function (usually a closed, bounded
interval) into finitely many subintervals (the partition)
- construct a simple function that has a constant value on each of
the subintervals of the partition (the Upper and Lower sums)
- take the limit of these simple functions as you add more and more
points to the partition.
If the limit exists it is called the Riemann integral and the
function is called Riemann integrable. Now we will take, in a manner of
speaking, the "opposite" approach:
- subdivide the range of the function into finitely many
pieces
- construct a simple function by taking a function whose values
are those finitely many numbers
- take the limit of these simple functions as you add more and
more points in the range of the original function
If the limit exists it is called the Lebesgue integral and the function is
called Lebesgue integrable. To define this new concept we use several steps:
- we define the Lebesgue Integral for "simple functions"
- we define the Lebesgue integral for bounded functions over sets
of finite measure
- we extend the Lebesgue integral to positive functions (that are not
necessarily bounded)
- we define the general Lebesgue integral
First, we need to
clarify what we mean by "simple function".
A function
f defined on a measurable set
A
that takes no more than finitely many distinct values
a1, a2, ... , an
can always be written as a simple function
f(x) = 
an
XAn(x)
where
An = { x 
A: f(x) = an }
Therefore simple functions can be thought of as dividing the
range of
f, where the resulting sets
An
may or may not be intervals.
| Examples 7.4.2: Simple Functions |
| |
A step function is a function s(x) such that
s(x) = cj for
xj-1 < x < xj
and the
{ xj } form a partition of [a, b].
Upper, Lower, and Riemann sums are examples of step functions.
What is the difference, if any, between step functions and simple
functions.
-
Are simple functions uniquely determined? In other words, if s1
and s2 are two simple functions with
s1(x) = s2(x), do they have to have
the same representation? If different representations are possible, which
one is "the best"?
-
How does the Dirichlet function fit in with this terminology?
-
Is the function that is equal to 1 if x is part of the Cantor
middle-third set and 0 otherwise a simple function?
-
Are sums, differences, and products of simple functions simple?
|
For simple functions we define the Lebesgue integral as follows:
| Example 7.4.4: Lebesgue Integral for Simple Functions |
| |
-
Find the Lebesgue integral of the constant function f(x) = c
over the interval [a, b].
-
Find the Lebesgue integral of a step function, i.e. a function
s such that
s(x) = cj for
xj-1 < x < xj
and the
{ xj } form a partition of [a, b].
-
Find the Lebesgue integral of the Dirichlet function restricted to
[0, 1] and of the characteristic function of the Cantor
middle-third set.
-
Define two simple functions
s1(x) = 2 X[0, 2](x) + 4 X[1, 3](x)
s2(x) = 2 X[0, 1)(x) + 6 X[1, 2](x) + 4 X(2, 3](x)
Show that s1(x) = s2(x) and
 s1(x) dx =
s2(x) dx.
-
We have seen before that the representation of a simple function is
not unique. Show that the Lebesgue integral of a simple function is independent
of its representation.
|
Just as step functions were used to define the Riemann integral of a bounded
function
f over an interval
[a, b], simple functions
are used to define the Lebesgue integral of
f over a set of finite
measure.
| Definition 7.4.5: Lebesgue Integral for Bounded Function |
| |
Suppose f is a bounded function defined on a measurable set
E with finite measure. Define the upper and lower
Lebesgue integrals, respectively, as
I*(f)L =
inf{ s(x) dx: s
is simple and
s  f }
I*(f)L =
sup{ s(x) dx: s
is simple and
s  f }
If I*(f)L = I*(f)L
the function f is called Lebesgue integrable over E
and the Lebesgue integral of f over E is denoted by
E f(x) dx
|
| Examples 7.4.6: Lebesgue Integral for Bounded Functions |
| |
-
Is the function f(x) = x Lebesgue integrable over
[0, 1]? If so, find the integral.
-
Is the function f(x) = x2 Lebesgue integrable over the
rational numbers inside [0, 2]? If so, find the integral.
-
Is the Dirichlet function restricted to [0, 1] Lebesgue
integrable? If so, find the integral.
-
Is every bounded function Lebesgue integrable?
|
Now a function
f can be integrated (if it is integrable) using
either the Riemann or the Lebesgue integral. Fortunately, for many simple
functions the two integrals agree and the Lebesgue integral is indeed a
generalization of the Riemann integral.
For most practial applications this theorem is all that is necessary:
for continuous functions or bounded functions with at most countably many
discontinuities over intervals
[a, b] there is no need to
distinguish between the Lebesgue or Riemann integral. All integration
techniques we learned apply equally well, using either integral. But
for more complicated situations or more theoretical purposes the Lebesgue
integral is more useful, but then techniques such as integration by parts or
substitution may no longer apply.
| Example 7.4.8: Riemann implies Lebesgue Integrable |
| |
-
Find the Lebesgue integral of f(x) = x cos(x) over the interval
[-1, 1].
-
Show that the converse of the above theorem is false, i.e. not every
bounded Lebesgue integrable function is Riemann integrable.
-
If possible, find the Riemann and Lebesgue integrals of the constant function
f(x) = 1 over the Cantor middle-third set.
-
Show that the restriction of a bounded continuous function to a measurable
set is Lebesgue integrable.
|
The Lebesgue integral has properties similar to
those of the Riemann integral,
but it is "more forgiving": you can change a function on a set of measure
zero without changing the integral at all.
| Examples 7.4.10: Properties of the Lebesgue Integral |
| |
-
Is the function f(x) = x ex Lebesgue integrable over
the Cantor middle-third set? If so, find the integral.
-
If f is Lebesgue integrable over E and
A f(x) B
then show that
A m(E) E f(x) dx
B m(E)
-
Suppose f is a bounded, non-negative function defined on a measurable
set E with finite measure and
F
 E
is measurable with
m(F) m(E).
Then show that
F f(x) dx
E f(x) dx
-
Suppose f is a bounded, non-negative function defined on a measurable
set E with finite measure such that
E f(x) dx = 0.
Show that f must then be equal to zero except on a set of
measure zero.
|
.
| Examples 7.4.11: Lebesgue is more general than Riemann |
| |
-
What happens when you change the value of a Lebesgue integrable function
at a single point?
-
Is it true that a function that is constant except at countably many points
is Lebesgue integrable?
-
What is the difference between Lebesgue integrable functions and bounded
continuous functions?
-
Can you take a Lebesgue integral over anything else but an interval?
-
Could you define a Lebesgue integral of a function whose domain is not
R?
|
But we can continue to extend the Lebesgue integral to functions that are
unbounded, including functions that may occasionally be
equal to
infinity. To do that, we first need to define the concept of a measurable
function.
| Definition 7.4.12: Measurable Function |
| |
Let f be a function from
E R
into
R 
{ - , }
. The function f is called (Lebesgue) measurable if
- the domain E of the function is a measurable set
- for every real number a the set
f -1 (-, a)
is a measurable set
|
In other words, functions whose values are real numbers or possibly plus or
minus infinity are measurable if the inverse image of every interval
(-, a) is measurable.
That is somewhat comparable to
one of the equivalent definitions
of continuous functions: a function f is continuous if the
inverse image of every open interval is open. However, not every measurable
function is continuous, while every continuous function is clearly measurable.
| Example 7.4.13: Measurable Functions |
| |
-
Show that every continuous function is measurable
-
Show that not every measurable function is continuous
-
If f is measurable and f = g except on a set of
measure zero, show that g is also measurable.
-
Show that a function f is measurable if and only if
- the set { x: f(x) < a } is measurable for all a
- the set { x: f(x) a } is measurable for all a
- the set { x: f(x) > a } is measurable for all a
- the set { x: f(x) a } is measurable for all a
-
Show that if f is measurable, then the set
{ x: f(x) = a } is measurable for all a
-
Is it true that if E is open and f is a
measurable function, then f -1(E) is also
measurable?
-
Is it true that if E is measurable and f is a
measurable function, then f -1(E) is also
measurable?
|
Measurable functions that are bounded are equivalent to Lebesgue integrable
functions.
Measurable functions do not have to be continuous, they may be unbounded and
they can, in particular, be equal to plus or minus infinity. On the other
hand, measurable functions are "almost" continous.
Using measurable functions allows us to extend the Lebesgue integral first to
non-negative functions that are not necessarily bounded and then to general
measurable functions.
| Examples 7.4.17: Lebesgue Integral of Non-Negative Function |
| |
-
Can a function that is equal to infinity at one or more points be
Riemann integrable?
-
Can a function that is equal to infinity at one or more points be
Lebesgue integrable?
-
What can you say about the set where a function f is equal to
infinity, if f is Lebesgue integrable?
-
Suppose f is a non-negative integrable function such that
E f(x) dx = 0.
Show that then f = 0 except on a set of measure zero.
|
The final step to define the Lebesgue integral of a general function is
now easy.
| Definition 7.4.18: The General Lebesgue Integral |
| |
Let f be a measurable function and define the positive and
negative parts of f, respectively, as:
f +(x) = max(f(x), 0)
f -(x) = max(-f(x), 0)
so that f = f + - f -. Then f
is Lebesgue integral if f + and
f - are Lebesgue integrable and
E f(x) dx =
E f +(x) dx -
E f -(x) dx =
|
Proposition 7.4.X remains true for general Lebegues integrable functions.
| Examples 7.4.19: The General Lebesgue Integral |
| |
Suppose that f is an integrable function over a set E,
and take any  > 0. Show that
-
There exists a simple function s such that
E | f - s | dx
<
-
There exists a step function s such that
E | f - s | dx
<
-
There exists a continuous function s such that
E | f - s | dx
<
|
Interactive Real Analysis
- part of 
Proof
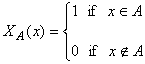
f(x) dx =