7.4. Lebesgue Integral

Example 7.4.4(e): Lebesgue Integral for Simple Functions

We have seen before that the representation of a simple function is not unique. Show that the Lebesgue integral of a simple function is independent of its representation.
We have to show that if s is a simple function with two different representations, then the integrals using either representation agree.

First assume that there are two representations for s

sA(x) = aj XAj(x) with Aj disjoint and aj not zero
sB(x) = bk XBk(x) with Bk disjoint and bk not zero
such that sA(x) = sB(x). Let's assume that the integral of s using the first representation exists, i.e. the measure of all sets Aj is finite.

If x Bk then x must be contained in one of the Aj's because otherwise sB(x) # 0 and sA(x) = 0. Therefore Bk Aj so that m(Bk) is finite for all k so that sB is integrable.

By the same reasoning we have

Bk = j ( Aj Bk ) and Aj = k ( Bk Aj )
If Aj Bk is not empty, then for x Aj Bk we have
aj = sA(x) = sB(x) = bk
so that aj = bk in that case. Putting everything together gives:
so that the integrals agree regardless of the representation.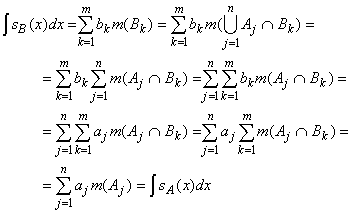

It remains to show that the integral of a simple function agrees with the integral over the canonical representation of that function, i.e. when the sets are disjoint and the coefficients are not zero.

Next | Previous | Glossary | Map