7. The Integral
7.3. Measures
The Riemann integral is certainly useful (and complicated) enough, but it does have a few limitations and oddities:| Examples 7.3.1:Oddities of Riemann Integral | |
| |
We therefore want to define another concept of integration that is more general than the Riemann integral, yet retains the "good" properties of that integral.
One of the limitations of the Riemann integral is that it is based on the concept of an "interval", or rather on the length of subintervals [xj-1, xj]. We therefore need to find a generalization of the "length" concept of a set in the real line. That new "length" concept, which we will call "measure", should satisfy two key conditions:
To define what will eventually be called Lebesgue Measure, we follow a two-stage strategy:
- The new "measure" concept should be applicable to intervals, unions of intervals, and to more general sets (such as a Cantor set). Ideally, it should be defined for all sets.
- The new "measure" concept should share as many properties as possible with the standard length of an interval, such as:
- the 'measure' of a set should be non-negative
- the 'measure' of an interval should be the length of that interval
- the 'measure' of countably many disjoint sets should be the sum of the 'measures' of the individual sets
- Stage One:
- We will define a concept extending length that is defined for all sets (to satisfy condition 1 above)
- Stage Two:
- We will modify that concept so that it looks as close as possible to the standard length concept (to satisfy condition 2 above)
| Definition 7.3.2: Outer Measure | |
The outer measure m* is a real-valued set function defined on a space X with the
properties:
| |
There are many examples of outer measures. The one that will be particularly useful for us is called Lebesgue Outer Measure, defined as follows:
| Definition 7.3.3: Lebesgue Outer Measure | |
If A is any subset of R, define the (Lebesgue) outer
measure of A as:
m*(A) = inf {where the infimum is taken over all countable collections of open intervals An such that A 
 An
and l(An) is the standard length of the
interval An. An
and l(An) is the standard length of the
interval An.
| |
This is quite a definition. First, you need to find an "open cover" of a set A by intervals An, which simply means that the union of the An cover the set A. That union, by the way, could involve finitely or countably many intervals. Then you need to find the (possibly infinite) sum of the lengths of all these intervals. Finally, you need to find the smallest such sum, taking all possible coverings of A into account. Still confused? I don't blame you, so it's time for some examples:
| Examples 7.3.4: Lebesgue Outer Measure | |
| |
Technically, we have to prove that the Lebesgue outer measure really is an outer measure, i.e. it does have the properties of an outer measure defined above. But the previous example actually proves conditions (1) to (3), while condtion (4) is left as a (technical and tricky) exercise.
We will not really talk about any other outer measure in this chapter, so whenever we say "outer measure" we really mean "Lebesgue outer measure". It turns out by the above examples that the Lebesgue outer measure has the property that m*([a,b]) = m*((a,b)) = b-a, i.e. the Lebesgue outer measure of any interval is its length.
| Definition 7.3.5: Measure | |
A measure is a non-negative set function defined on a sigma-algebra of sets such that the measure of the empty set is zero
and the additional property that it is countably additive, i.e.
m( Aj) = Aj) =
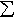 m(Aj)
for any pairwise disjoint sets Aj. m(Aj)
for any pairwise disjoint sets Aj.
| |
So, a measure is an outer measure with a domain that no longer consists of all subsets of a space X but is defined on a sigma-algebra of subsets of X, but which is countably additive instead of countably subadditive. The monotonicty property (3) of an outer measure is implied (see example below).
| Definition 7.3.6: Sigma Algebra and Measure Space | |
|
A sigma algebra is a collection of subsets of a space X that is closed under complements and countable unions,
i.e. the complement of any member of the sigma algebra is again part of the sigma algebra, and the countable union of sets
from the sigma algebra is again part of it.
A measure space (X, Σ, m) is a space X together with a sigma algbra Σ of subsets of X and a measure m defined on the sigma-algebra. | |
There are many measures and outer measures:
Example 7.3.7: Measures
| |
|
| |||
The goal now is to restrict the (Lebesgue) outer measure only to those sets for which it becomes countably additive. This definition is due to Caratheodory. It is relatively straight-forward, but it is not immediately clear as to where his idea comes from.
| Definition 7.3.8: Measurable Sets (according to Caratheodory) | |
A set E is called measurable if for every set A we have that
m*(A) = m*(Awhere * is an outer measure. For a measurable set we define the measure of E as m(E) = m*(E). | |
Note: Since
A = (A  E)
E)  (A
(A  Ec)
we have by subadditivity
m*(A) ≤ m*(A
Ec)
we have by subadditivity
m*(A) ≤ m*(A  E) + m*(A
E) + m*(A  Ec)
Therefore a set E is measurable if
m*(A) ≥ m*(A
Ec)
Therefore a set E is measurable if
m*(A) ≥ m*(A  E) + m*(A
E) + m*(A  Ec)
since the other inequality comes for free. As it will turn out, the measurable sets are those sets for which the outer measure becomes additive.
Ec)
since the other inequality comes for free. As it will turn out, the measurable sets are those sets for which the outer measure becomes additive.
| Theorem 7.3.9: Properties of Measure | |
| |
Note that the above statements are true for any measure, whereas the next theorem applies to Lebesgue measure in particular.
| Definition 7.3.10: Lebesgue Measure | |
| If we restrict the Lebesgue outer measure to the measurable sets only, the resulting function is called Lebesgue measure. | |
Note: Another way to define a Lebesgue measurable set would be to define an inner measure m*. Where the outer measure of a set E involves the inf over all open coverings of E, the inner measure of a set E would be the sup over all compact subsets of E. Then we would call those sets measurable for which m*(E) = m*(E). That idea is rather symmetric and fairly straight-forward, but Caratheodory’s approach, while less intuitive, is less abstract and easier to work with, and applies to any outer measure.
We finally prove that moving from Lebesgue outer measure to Lebesgue measure achieves our goal of countable additivity.
| Theorem 7.3.11: Properties of Lebesgue Measure | |
| |
The last of the above properties is what we were after: we wanted the L-measure to be additive and we were willing to pay the price that a measure may not be defined for all subsets. In fact, our measure is defined only for the measurable sets.
After all this theory it is time to consider some easier examples, including the L-measure of some well-known sets that are not intervals (whose L-measure, as we know by now, are their length).
| Examples 7.3.12: Properties of Lebesgue Measure | |
| |
| Theorem 7.3.13: Non-Lebesgue measurable set | |
| |
Sometimes we refer to the collection of all open sets, closed sets, and sets that can be derived from them by taking union, intersecions, and complements as part of the Borel sets. But not every Borel set is a union or intersecion of open/closed sets, and unions/intersecions of those, etc., so that the Borel sets are really something new. In fact:
| Definition 7.3.14: Borel sets | |
| The Borel sets are the smallest sigma-algebra that contains the open sets. It includes complements, unions, and intersecions of open sets, and complements, intersecions, and unions of those sets, and so on. | |
Note: There are unaccountably many Borel sets, but there are not *that* many. In other words, card(Borel sets) = c. Compare this with the cardinality of all Lebesgue measurable sets, which is 2^c (why – see exercises). All Borel sets are (Lebesgue) measurable, but not all Lebesgue measurable sets are Borel sets. So, there are a lot of Lebesgue measurable sets and comparatively few Borel sets.
Before we are done, we need one more result:
| Proposition 7.3.15: Monotone Sequences of Measurable Sets | |
If { An } is a sequence of measurable sets
that is decreasing, i.e.
Aj  Aj+1
for all j, and m(A1) is
finite, then Aj+1
for all j, and m(A1) is
finite, then
lim m(Aj) = m(If { An } is a sequence of measurable sets that is increasing in the sense that Aj+1  Aj
for all j, then Aj
for all j, then
lim m(Aj) = m( | |
| Examples 7.3.16: Monotone sequences of measurable sets | |
| |
As our final result we show that Lebesgue measurable sets are "almost" open or "almost" closed:
| Theorem 7.3.17: Lebesgue Sets are almost open | |
If a set A is L-measurable then for any ε > 0 there exists an open set O
such that A  O and m(O-A) < ε
as well as a closed set F such that F O and m(O-A) < ε
as well as a closed set F such that F  A and
m(A-F) < ε. A and
m(A-F) < ε.
| |
To summarize, we introduced a new concept called measure in two stages, each of which had a typical "good news, bad news" property.
- In the first stage we defined outer measure.
- good news: outer measure is defined for all sets.
- bad news: outer measure is not additive, i.e. it is not quite comparable to a length.
- In the second stage we defined measure by restricting outer measure to the measurable sets.
- good news: measure is additive, i.e. it is a good generalization of length.
- bad news: measure is not defined for all sets
- Then we introduced concrete examples of outer measure - the Lebesgue outer measure - and of measure - the Lebesgue measure - and we studied their properties
 Interactive Real Analysis
Interactive Real Analysis if A is infinite. Show that that cm is a measure
(called counting measure).
if A is infinite. Show that that cm is a measure
(called counting measure).
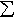 m(Aj)
m(Aj)