7.3. Measures
Examples 7.3.10(c): Properties of Measure
Recall the definition of the Cantor set: letA0 = [0, 1]and define, for each n, the sets An recursively as
An = An-1 \Then the Cantor set is given as:
C =We have already shown that the Cantor set has "length" zero, but the concept of length does not really apply since the Cantor set is not an interval. Now we can redo our previous calculations, but under the mathematically correct name of measure.An
First, the Cantor set is expressed as a combination of unions and intersections of intervals so that C is measurable. Let's compute the measure of the sets An:

A0 = [0, 1] so that m(A0) = 1

A1 = A0 - (1/3, 2/3) so that
m(A1) = m(A0) - m(1/3, 2/3) = 1 - 1/3

A2 = A1 - (1/9, 2/9) - (7/9, 8/9) so that
m(A2) = m(A1) - m(1/9, 2/9) - m(7/9, 8/9) = 1 - 1/3 - 2*1/9

A3 = A2 - (1/27, 2/27) - (7/27, 8/27) - (19/27, 20/25) - (25/27, 26/27) so thatIn general we have
m(A3) = 1 - 1/3 - 2*1/9 - 4*1/27
for all n. Since C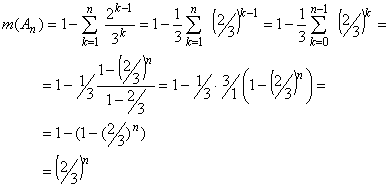
 An
for all n we have that
An
for all n we have that
m(C)for all n. Therefore m(C) = 0.(2/3)n
 Interactive Real Analysis
Interactive Real Analysis