7.4. Lebesgue Integral
Example 7.4.2(b): Simple Functions
Are simple functions uniquely determined? In other words, if s1
and s2 are two simple functions with
s1(x) = s2(x), do they have to have
the same representation? If different representations are possible, which
one is "the best"?
No, two simple functions can be the same but have different representations.
For example, take the sets
A = [0, 1] and B = (1, 2]where Q are the rationals and I are the irrationals. Then all sets are measurable. Define two simple functions
A' = AQ and A'' = A
I
B' = BQ and B'' = B
I
s1(x) = XA(x) + XB(x)Obviously the two simple functions have different representations, but s1(x) = s2(x) for all x. Note that s1 is a simple function as well as a step function, while s2 is not a step function.
s2(x) = XA' (x) + XA'' (x) + XB' (x) + XB'' (x)
Simple functions assume only finitely many values. If s is a simple function and { a1, ..., an } are the non-zero values of s, define the sets
Aj = { x: s(x) = aj }Then the sets { Aj } are all disjoint and
s(x) =Therefore, we can always assume without loss of generality that if s(x) =aj XAj(x)
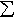 cj XEj(x)
is any simple function, the sets Ej are
disjoint and the numbers cj are not zero. This
representation (the sets are disjoint and the coefficients are non-zero) is
the canonical representation of a simple function.
cj XEj(x)
is any simple function, the sets Ej are
disjoint and the numbers cj are not zero. This
representation (the sets are disjoint and the coefficients are non-zero) is
the canonical representation of a simple function.
 Interactive Real Analysis
Interactive Real Analysis