7.4. Lebesgue Integral
Example 7.4.11(c): Properties of the Lebesgue Integral
Suppose f is a bounded, non-negative function defined on a measurable
set E with finite measure and
F  E
is measurable with
m(F)
E
is measurable with
m(F)  m(E).
Then show that
m(E).
Then show that
The proof is easy, using one of the properties of the Lebesgue integral ...
so it's of course left as an exercise.
 E
is measurable with
m(F)
E
is measurable with
m(F)  m(E).
Then show that
m(E).
Then show that
F f(x) dx

E f(x) dx
Hint:
F 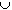 (E - F) = E
and
F and E - F are disjoint ...
(E - F) = E
and
F and E - F are disjoint ...
 Interactive Real Analysis
Interactive Real Analysis