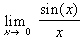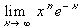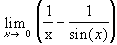6. Limits, Continuity, and Differentiation
6.5. Differentiable Functions
Having discussed continuity we will turn to another class of functions:
differentiable functions. This group of functions is one of the
focus points of Calculus, and you should already be familiar with
many aspects of those functions
In our setting these functions will play a rather minor role and
we will only briefly review the main topics of that theory. As
usual, proofs will be our focus point, rather than techniques
of differentiation as it has been in Calculus.
First, we will start with the definition of derivative.
The usual geometric interpretation of the derivative at a point
is as slope of the tangent line to the graph of
f(x) at the point
(c, f(c)). If a function is differentiable, it may not have any
'edges'. That often makes it easy to decide whether a function
is differentiable if you can see the graph of the function.
| Examples 6.5.2: |
| |
 Find the derivative of f(x) = x and of f(x) = 1 / x.
Find the derivative of f(x) = x and of f(x) = 1 / x.
 Find the derivative of
Find the derivative of 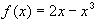
 Find the derivative of
Find the derivative of 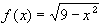
|
Another way to define a differentiable function is by saying that
f(x) can be approximated by a linear function, as in the following
theorem:
This theorem provides a suitable method to generalize the concept
of derivative to other spaces: a function defined in some general
space is called differentiable at a point
c if it can be approximated
by a linear function at that point. On the real line the linear
function
M ( x - c ) + f(c), of course, is the equation of the
tangent line to
f at the point
c. In higher dimensional real space
this concept is known as the
total derivative of a function.
| Examples 6.5.4: |
| |
 Why might our original definition of differentiability not be suitable for
functions of, say, two or three real variables ?
Why might our original definition of differentiability not be suitable for
functions of, say, two or three real variables ?
 Use the characterization of differentiability via approximation by linear
functions to define the concept of 'derivative' for functions of n real
variables.
Use the characterization of differentiability via approximation by linear
functions to define the concept of 'derivative' for functions of n real
variables.
|
In any case, differentiability is a new concept, so that we should
first ask ourselves what its relation to the previous concept
of continuity is.
| Examples 6.5.6: |
| |
 The function f(x) = | x | is continuous everywhere. Is it also differentiable
everywhere ?
The function f(x) = | x | is continuous everywhere. Is it also differentiable
everywhere ?
 The function f(x) = x sin(1/x) is continuous everywhere except at x = 0, where
it has a removable discontinuity. If the function is extended appropriately to
be continuous at x = 0, is it then differentiable at x = 0 ?
The function f(x) = x sin(1/x) is continuous everywhere except at x = 0, where
it has a removable discontinuity. If the function is extended appropriately to
be continuous at x = 0, is it then differentiable at x = 0 ?
 The function f(x) = x2 sin(1/x) has a removable
discontinuity at x = 0. If the function is extended appropriately to be
continuous at x = 0, is it then differentiable at x = 0 ?
The function f(x) = x2 sin(1/x) has a removable
discontinuity at x = 0. If the function is extended appropriately to be
continuous at x = 0, is it then differentiable at x = 0 ?
|
As with continuous functions, differentiable functions can be
added, multiplied, divided, and composed with each other to yield
again differentiable functions. In fact, there are easy rules
to compute the derivative of those new functions, all of which
are well- known from Calculus.
Next, we will state several important theorems for differentiable
functions:
| Theorem 6.5.8: Rolle Theorem |
| |
If f is continuous on [a, b] and differentiable on
(a, b), and f(a) = f(b) = 0, then there exists a number
x in (a, b) such that f'(x) = 0.
Proof
|
An extension of Rolle's theorem that removes the conditions on
f(a) and
f(b) is the Mean- Value-Theorem. It
is actually a 'shifted' version of Rolle's theorem, as its proof illustrates.
A more general version of the Mean Value theorem is also mentioned which is
sometimes useful.
| Theorem 6.5.9: Mean Value Theorem |
| |
If f is continuous on [a, b] and differentiable on
(a, b), then there exists a number c in (a, b)
such that
- f'(c) =
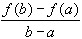
If f and g are continuous on [a, b] and
differentiable on (a, b) and g'(x) # 0 in (a, b)
then there exists a number c in (a, b) such that
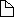
Proof
|
| Examples 6.5.10: |
| |
 Does Rolle's theorem apply to
Does Rolle's theorem apply to 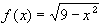 defined on (-3, 3) ? If so, find the number guarantied by the theorem to exist.
defined on (-3, 3) ? If so, find the number guarantied by the theorem to exist.
 Prove that if f is differentiable on R and | f'(x) |
Prove that if f is differentiable on R and | f'(x) |
 M for all x, then | f(x) - f(y) | M for all x, then | f(x) - f(y) |
 M | x - y | for all numbers x, y.
Functions that satisfy such an inequality are called Lipschitz functions. M | x - y | for all numbers x, y.
Functions that satisfy such an inequality are called Lipschitz functions.
 Use the Mean Value theorem to show that
Use the Mean Value theorem to show that
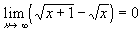
|
Rolle's theorem and the Mean Value theorem allow us to develop
the familiar test for local extrema of a function, as well as
increasing and decreasing functions. Recall the definition of
local extremum:
| Definition 6.5.11: Local Extremum |
| |
Let f be a function defined on a domain D, and c
a point in D.
- If there exists a neighborhood U of c with f(c)
 f(x) for all x in U, then f(c) is called
a local maximum for the function f that occurs at x = c. f(x) for all x in U, then f(c) is called
a local maximum for the function f that occurs at x = c.
- If there exists a neighborhood U of c with f(c)
 f(x) for all x in U, then f(c) is called
a local minimum for the function f that occurs at x = c. f(x) for all x in U, then f(c) is called
a local minimum for the function f that occurs at x = c.
- If f(x) has either a local minimum or a local maximum at x = c, then
f(c) is called local extremum of the function f.
|
You can find possible local extrema by applying the following theorem:
| Theorem 6.5.12: Local Extrema and Monotonicity |
| |
- If f is differentiable on (a, b), and f has a local extrema at x = c, then
f'(c) = 0.
- If f'(x) > 0 on (a, b) then f is increasing on (a, b).
- If f'(x) < 0 on (a, b) then f is decreasing on (a, b).
Proof
|
This theorem suggests the following table in order to find local
minima and maxima: Suppose you have found a point c such that
f'(c) either does not exist or f'(c) = 0. For each c (called a
critical point of f) we may have one of these four situations:
| Loc. Max |
| interval | (a, c) | (c , b) |
| sign of f'(x) | + | - |
| dir. of f(x) | up | down |
|
| Loc. Min |
| interval | (a, c) | (c , b) |
| sign of f'(x) | - | + |
| dir. of f(x) | down | up |
|
| No Extremum |
| interval | (a, c) | (c , b) |
| sign of f'(x) | + | + |
| dir. of f(x) | up | up |
|
| No Extremum |
| interval | (a, c) | (c , b) |
| sign of f'(x) | - | - |
| dir. of f(x) | down | down |
|
The results of these tables can be summarized in the following:
| Corollary 6.5.13: Finding Local Extrema |
| |
Suppose f is differentiable on (a, b). Then:
- If f'(c) = 0 and f'(x) > 0 on (a, x) and f'(x) < 0 on (x, b), then
f(c) is a local maximum.
- If f'(c) = 0 and f'(x) < 0 on (a, x) and f'(x) > 0 on (x, b), then
f(c) is a local minimum.
Proof
|
These results above are the cornerstones of Calculus 1 in most
colleges. As a review, you may enjoy the following examples:
| Examples 6.5.14: |
| |
 If f(x) = x3 -2 x2,
then find all local extrema.
If f(x) = x3 -2 x2,
then find all local extrema.
 If
f(x) = | 1 - x2|, then find all relative extrema. If
f(x) = | 1 - x2|, then find all relative extrema.
|
One of the nice applications of derivatives is that they give
an easy short-cut rule to finding limits, when those limits are
difficult to obtain otherwise.
There are other situations where l'Hospital's rule may apply, but
often expressions can be rewritten so that one of these two cases
will apply.
| Examples 6.5.16: |
| |
- Please find the following limits, using, if necessary, l'Hospital's rules:

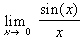

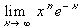

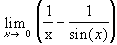
|
 Interactive Real Analysis
Interactive Real Analysis
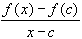
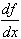 or
or
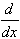 f(x).
f(x).
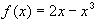
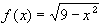
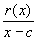 = 0
= 0
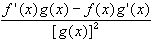
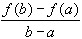
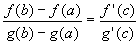
 M for all x, then | f(x) - f(y) |
M for all x, then | f(x) - f(y) |
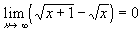
 f(x) for all x in U, then f(c) is called
a local maximum for the function f that occurs at x = c.
f(x) for all x in U, then f(c) is called
a local maximum for the function f that occurs at x = c.
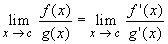 ,
provided the limit on the right exists.
,
provided the limit on the right exists.
 f(x) =
f(x) =
 ,then
,then
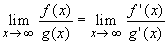 ,
provided the last limit exists
,
provided the last limit exists