6.5. Differentiable Functions
Examples 6.5.10(a):
Does Rolle's theorem apply to 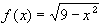 defined on (-3, 3) ? If so, find the number guarantied by the theorem
to exist.
defined on (-3, 3) ? If so, find the number guarantied by the theorem
to exist.
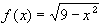 defined on (-3, 3) ? If so, find the number guarantied by the theorem
to exist.
defined on (-3, 3) ? If so, find the number guarantied by the theorem
to exist.
| This function is continuous on the interval [-3, 3], and differentiable on (-3, 3). It is not differentiable at x = -3 and x = +3, but Rolle's theorem does not require the function to be differentiable at the endpoints. Also, f(3) = f(-3) = 0. Therefore, Rolle's theorem does apply. |
It guaranties the existence of a number c between -3 and 3 such that f'(c) = 0. It does not specify where exactly this number is located. However, a quick calculation shows that the number c is in fact c = 0.
 Interactive Real Analysis
Interactive Real Analysis