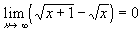6.5. Differentiable Functions
Examples 6.5.10(c):
Define the function f(x) =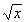 .
Then f is continuous on [0,
.
Then f is continuous on [0,  )
and differentiable on (0,
)
and differentiable on (0,  ).
By the Mean Value theorem there exists a number c such that
).
By the Mean Value theorem there exists a number c such that
for c between x and x + 1. But then= f'(c)
0 <As x goes to infinity, so does c (it is always bigger than x). The left side of this equation goes to 0 as c goes to infinity. Therefore, the right side must also go to zero.-
= 1/2 * 1 /
 Interactive Real Analysis
Interactive Real Analysis