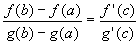6.5. Differentiable Functions
Theorem 6.5.9: Mean Value Theorem
f'(c) =If f and g are continuous on [a, b] and differentiable on (a, b) and g'(x) # 0 in (a, b) then there exists a number c in (a, b) such that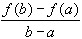
Proof:
The first version of the Mean Value theorem is actually Rolle's theorem in disguise. A simple linear function can convert one situation into the other:
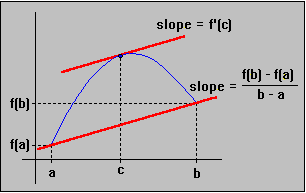 geometric interpretation
of MVT
geometric interpretation
of MVT
We need a linear function (linear so that we can easily compute its derivative) that maps the line through the two points ( a, f(a) ) and ( b, f(b) ) to the points ( a, 0 ) and ( b, 0 ). If we subtract that map from the function we will be in a situation where we can apply Rolle's theorem.
To find the equation of such a line is easy:
- y - f(a) =
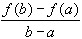 (
x - a )
(
x - a )
Thus, we define the following function:
- h(x) = f(x) -
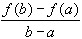 (
x - a ) - f(a)
(
x - a ) - f(a)
Then h is differentiable in ( a, b ) with h(a) = h(b) = 0. Therefore, Rolle's theorem guaranties a number c between a and b such that h'(c) = 0. But then
- 0 = h'(c) = f'(c) -
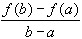
which is exactly what we had to show for the first part.
The second part is very similar. You can fill in the details yourself by considering the function
- h(x) = f(x) -
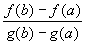 (
g(x) - g(a) ) - f(a)
(
g(x) - g(a) ) - f(a)

 Interactive Real Analysis
Interactive Real Analysis