3. Sequences of Numbers
3.4. Lim Sup and Lim Inf
When dealing with sequences there are two choices:
- the sequence converges
- the sequence diverges
| Definition 3.4.1: Lim Sup and Lim Inf | |
Let  be a sequence of real
numbers. Define be a sequence of real
numbers. Define
Aj = inf{aj , aj + 1 , aj + 2 , ...}and let c = lim (Aj). Then c is called the limit inferior of the sequence  . .
Let Bj = sup{aj , aj + 1 , aj + 2 , ...}and let c = lim (Bj). Then c is called the limit superior of the sequence  . .
In short, we have:
| |
| Proposition 3.4.3: Lim inf and Lim sup exist | |
| lim sup and lim inf always exist (possibly infinite) for any sequence of real numbers. | |
It is important to try to develop a more intuitive understanding about lim sup and lim inf. The next results will attempt to make these concepts somewhat more clear.
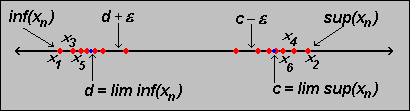
| Proposition 3.4.4: Characterizing lim sup and lim inf | |
Let  be an arbitrary
sequence and let
c = lim sup(aj) and
d = lim inf(aj).
Then be an arbitrary
sequence and let
c = lim sup(aj) and
d = lim inf(aj).
Then
 > 0 there are arbitrary large
j such that
aj > c - > 0 there are arbitrary large
j such that
aj > c -  and arbitrary large k such that
ak < d +
and arbitrary large k such that
ak < d + 
| |
A little bit more colloquial, we could say:
- Aj picks out the greatest lower bound for the truncated sequences {aj}. Therefore Aj tends to the smallest possible limit of any convergent subsequence.
- Similarly, Bj picks the smallest upper bound of the truncated sequences, and hence tends to the greatest possible limit of any convergent subsequence.
The final statement relates lim sup and lim inf with our usual concept of limit.
| Proposition 3.4.6: Lim sup, lim inf, and limit | |
If a sequence {aj} converges then
lim sup aj = lim inf aj = lim ajConversely, if lim sup aj = lim inf aj are both finite then {aj} converges. | |
To see that even simple concepts like lim inf and lim sup can result in interesting math consider the following unproven conjecture:
If pn is the n-th prime number, then lim inf pn+1 - pn = 2 and lim sup pn+1 - pn =
The first equation is a conjecture, not yet proven, called the twin prime conjecture. In fact, it is not even known if the lim inf is finite. On the other hand, the second equation involving lim sup is known to be infinite because of arbitrary spaces between two primes.
 Interactive Real Analysis
Interactive Real Analysisj}.gif) ?
?
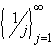 ?
?
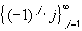
 lim inf
lim inf 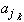
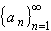 is the
sequence of all rational numbers in the interval [0, 1], enumerated in
any way, find the lim sup and lim inf of that sequence.
is the
sequence of all rational numbers in the interval [0, 1], enumerated in
any way, find the lim sup and lim inf of that sequence.