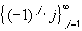• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 3.1. Sequences
• 3.2. Cauchy Sequences
• 3.3. Subsequences
• 3.4. Lim Sup and Lim Inf
• 3.5. Special Sequences
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

3.4. Lim Sup and Lim Inf

Examples 3.4.2(c):

This sequence is {-1, 2, -3, 4, -5, 6, -7, ...}. You can quickly check, by looking at the definition of lim inf and lim sup and working out the numbers A_j and B_j that:

• inf { (-1) ^j j } = -
• lim inf { (-1) ^j j } = -
• sup{ (-1) ^j j } =
• lim sup{ (-1) ^j j } =

Note that while lim sup and lim inf are not real numbers, they are uniquely defined as plus or minus infinity. The limit of the original sequence, on the other hand, does not exist at all.

Hence, there is a difference between a limit not existing, and a limit that approaches infinity. In the latter sense, lim inf and lim sup will always exist, which is their most useful property.

Interactive Real Analysis, ver. 2.0.1(c)
(c) 1994-2018, Bert G. Wachsmuth
Page last modified: Apr 25, 2024