3. Sequences of Numbers
3.3. Subsequences
So far we have learned the basic definitions of a sequence (a function
from the natural numbers to the Reals), the concept of convergence, and
we have extended that concept to one which does not pre-suppose the unknown
limit of a sequence (Cauchy sequence).
Unfortunately, however, not all sequences converge. We will now introduce
some techniques for dealing with those sequences. The first is to change the
sequence into a convergent one (extract subsequences) and the second is to
modify our concept of limit (lim sup and lim inf).
| Definition 3.3.1: Subsequence |
| |
Let  be a sequence. When we
extract from this sequence only certain elements and drop the remaining ones we
obtain a new sequences consisting of an infinite subset of the original sequence.
That sequence is called a subsequence and denoted by be a sequence. When we
extract from this sequence only certain elements and drop the remaining ones we
obtain a new sequences consisting of an infinite subset of the original sequence.
That sequence is called a subsequence and denoted by
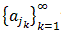
|
One can extract infinitely many subsequences from any given sequence.
| Examples 3.3.2: |
| |
 Take the sequence
Take the sequence j}.gif) ,
which we have proved does not converge. Extract every other member, starting with
the first. Does this sequence converge ? What if we extract every other member,
starting with the second. What do you get in this case ? ,
which we have proved does not converge. Extract every other member, starting with
the first. Does this sequence converge ? What if we extract every other member,
starting with the second. What do you get in this case ?
 Take the sequence
Take the sequence 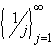 .
Extract three different subsequences of your choice. Do these
subsequences converge ? Is so, to what limit ? .
Extract three different subsequences of your choice. Do these
subsequences converge ? Is so, to what limit ?
|
The last example is an indication of a general result:
| Proposition 3.3.3: Subsequences from Convergent Sequence |
| |
If  is a convergent sequence,
then every subsequence of that sequence converges to the same limit is a convergent sequence,
then every subsequence of that sequence converges to the same limit
If  is a sequence such that every
possible subsequence extracted from that sequences converge to the same limit, then
the original sequence also converges to that limit. is a sequence such that every
possible subsequence extracted from that sequences converge to the same limit, then
the original sequence also converges to that limit.
Proof
|
The next statement is probably one on the most fundamental results of basic real
analysis, and generalizes the above proposition. It also explains why subsequences
can be useful, even if the original sequence does not converge.
| Example 3.3.5: |
| |
 Does
Does }.gif) converge ?
Does there exist a convergent subsequence ? What is that subsequence ? converge ?
Does there exist a convergent subsequence ? What is that subsequence ?
 In fact, the following is true: given any number L between -1 and 1,
it is possible to extract a subsequence from the sequence
In fact, the following is true: given any number L between -1 and 1,
it is possible to extract a subsequence from the sequence
}.gif) that converges to L.
This is difficult to prove. that converges to L.
This is difficult to prove.
|
Next, we will broaden our concept of limits.
 be a sequence. When we
extract from this sequence only certain elements and drop the remaining ones we
obtain a new sequences consisting of an infinite subset of the original sequence.
That sequence is called a subsequence and denoted by
be a sequence. When we
extract from this sequence only certain elements and drop the remaining ones we
obtain a new sequences consisting of an infinite subset of the original sequence.
That sequence is called a subsequence and denoted by
 is a convergent sequence,
then every subsequence of that sequence converges to the same limit
is a convergent sequence,
then every subsequence of that sequence converges to the same limit
 be a sequence of real
numbers that is bounded. Then there exists a subsequence
be a sequence of real
numbers that is bounded. Then there exists a subsequence
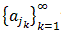 that converges.
that converges.
 Interactive Real Analysis
Interactive Real Analysisj}.gif) ,
which we have proved does not converge. Extract every other member, starting with
the first. Does this sequence converge ? What if we extract every other member,
starting with the second. What do you get in this case ?
,
which we have proved does not converge. Extract every other member, starting with
the first. Does this sequence converge ? What if we extract every other member,
starting with the second. What do you get in this case ?
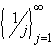 .
Extract three different subsequences of your choice. Do these
subsequences converge ? Is so, to what limit ?
.
Extract three different subsequences of your choice. Do these
subsequences converge ? Is so, to what limit ?
}.gif) converge ?
Does there exist a convergent subsequence ? What is that subsequence ?
converge ?
Does there exist a convergent subsequence ? What is that subsequence ?