3.3. Subsequences
Theorem 3.3.4: Bolzano-Weierstrass
Let  be a sequence
of real numbers that is bounded. Then there exists a subsequence
be a sequence
of real numbers that is bounded. Then there exists a subsequence
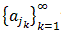 that converges.
that converges.
 be a sequence
of real numbers that is bounded. Then there exists a subsequence
be a sequence
of real numbers that is bounded. Then there exists a subsequence
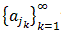 that converges.
that converges.
Proof:
Since the sequence is bounded, there exists a number M such that | aj | < M for all j. Then:either [-M, 0] or [0, M] contains infinitely many elements of the sequenceSay that [0, M] does. Choose one of them, and call it
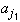
either [0, M/2] or [M/2, M] contains infinitely many elements of the (original) sequence.Say it is [0, M/2]. Choose one of them, and call it
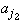
either [0, M/4] or [M/4, M/2] contains infinitely many elements of the (original) sequenceThis time, say it is [M/4, M/2]. Pick one of them and call it
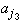
Keep on going in this way, halving each interval from the previous step at the next step, and choosing one element from that new interval. Here is what we get:
- |
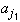 -
-
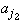 | < M,
because both are in [0, M]
| < M,
because both are in [0, M]
- |
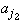 -
-
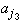 | < M / 2,
because both are in [0, M/2]
| < M / 2,
because both are in [0, M/2]
- |
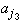 -
-
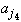 | < M / 4,
because both are in [M/2, M/4]
| < M / 4,
because both are in [M/2, M/4]
|because both are in an interval of length M / 2k-1. So, this proves that consecutive elements of this subsequence are close together. That is not enough, however, to say that the sequence is Cauchy, since for that not only consecutive elements must be close together, but all elements must get close to each other eventually.-
| < M / 2k-1
So: take any  > 0, and
pick an integer N such that
???...??? (This trick is often used: first, do some calculation, then
decide what the best choice for N should be. Right now, we
have no way of knowing a good choice). Pretending, however, that we knew
this choice of N, we continue the proof. For any
k, m > N (with m > k) we have:
> 0, and
pick an integer N such that
???...??? (This trick is often used: first, do some calculation, then
decide what the best choice for N should be. Right now, we
have no way of knowing a good choice). Pretending, however, that we knew
this choice of N, we continue the proof. For any
k, m > N (with m > k) we have:
Now we can see the choice for N: we want to make is so large, such that whenever k, m > N, the difference between the members of the subsequence is less than the prescribed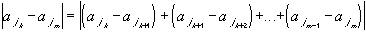
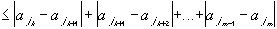
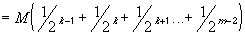
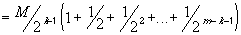
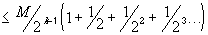
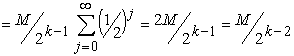
 . What is therefore the right choice
for N to finish the proof ?
. What is therefore the right choice
for N to finish the proof ?

 Interactive Real Analysis
Interactive Real Analysis