3.4. Lim Sup and Lim Inf
Example 3.4.5:
If 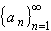 is the sequence
of all rational numbers in the interval [0, 1], enumerated in any way,
find the lim sup and lim inf of that sequence.
is the sequence
of all rational numbers in the interval [0, 1], enumerated in any way,
find the lim sup and lim inf of that sequence.
Since the numbers 1 and 0 are itself rational numbers, it is clear that
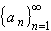 is the sequence
of all rational numbers in the interval [0, 1], enumerated in any way,
find the lim sup and lim inf of that sequence.
is the sequence
of all rational numbers in the interval [0, 1], enumerated in any way,
find the lim sup and lim inf of that sequence.
sup{ an } = 1 and inf{ an } = 0 Therefore, we already know that0To find the lim sup, we will construct a subsequence that converges to 1:lim inf{ an }
lim sup{ an }
1
These numbers exist because the rational numbers in the interval [0, 1] are arbitrarily close to any real number in that interval, according to the Density principle.
- there exists 0 < aj1 < 1 with 1 - aj1 < 1
- there exists 0 < aj2 < 1 with 1 - aj2 < 1/2 and aj1 # aj2
- there exists 0 < aj3 < 1 with 1 - aj3 < 1/3 and aj3 different from the previous ones
- and so on ...
The subsequence { ajk } constructed in the above way converges to 1. We already know that any limit of any convergent subsequence must be less than or equal to 1. Therefore, since the lim sup is the greatest limit of any convergent subsequence, we have
lim sup { an } = 1Similarly, we can extract a subsequence { ajk } that converges to 0. We also know that every limit of any convergent subsequence must be greater or equal to zero. Therefore, since the lim inf is the smallest possible limit of all convergent subsequence, we have:lim inf { an } = 0
 Interactive Real Analysis
Interactive Real Analysis