7.1. Riemann Integral
Corollary 7.1.20: Integral Evaluation Shortcut
Suppose f is an continuous function defined on the
closed, bounded interval [a, b], and G
is a function on [a, b] such that
G'(x) = f(x) for all x in (a, b).
Then
Note: The function G is often called Antiderivative of f, and this corollary is called First Fundamental Theorem of Calculus in many calculus text books. Those books also define a Second Fundamental Theorem of Calculus, which we called the Fundamental Theorem of Calculus.f(x) dx = G(b) - G(a)
Proof:
This being a corollary means that it must be easy to prove. We already know from the previous theorem that if we define the functionF(x) =then F(b) - F(a) =f(t) dt
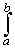 f(x) dx
and F' = f. What we need to prove is that if we take
any function G such that G'(x) = f(x)
then G(b) - G(a) =
f(x) dx
and F' = f. What we need to prove is that if we take
any function G such that G'(x) = f(x)
then G(b) - G(a) = 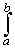 f(x) dx
also. So, define
f(x) dx
also. So, define
H(x) = F(x) - G(x)where F and G are as defined above. Then
H'(x) = F'(x) - G'(x) = f(x) - f(x) = 0so that H(x) = c for some constant c. But then F(x) = G(x) + c so that
F(b) - F(a) = (G(a) + c) - (G(b) + c) = G(b) - G(a)
 Interactive Real Analysis
Interactive Real Analysis