7.1. Riemann Integral
Theorem 7.1.19: Fundamental Theorem of Calculus
Suppose f is a bounded, integrable function defined on the
closed, bounded interval [a, b], define a new function:
F(x) =Then F is continuous in [a, b]. Moreover, if f is also continuous, then F is differentiable in (a, b) andf(t) dt
F'(x) = f(x) for all x in (a, b).
Note: In many calculus texts this theorem is called the Second fundamental theorem of calculus. Those books also define a First Fundamental Theorem of Calculus.
Proof:
The first assumption is simple to prove: Take x and c inside [a, b]. Since f is bounded we know that | f(x) | < M for some number M. By the properties of the Riemann integral we know:assuming without loss of generality that c > x. But then we can take the limit as x approaches c to see that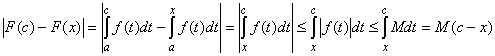
which implies continuity of F at x = c.| F(x) - F(c) | = 0
Now we want to prove that F(x) is differentiable with F' = f if f is continuous.
Pick x inside the interval (a, b) and choose a number h so small that x+h is also in (a, b). We compute the difference quotient:
and define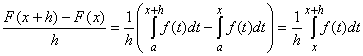
m = inf{ f(t), tClearly we have that m[x, x+h] }
M = sup{ f(t), t[x, x+h] }
 f(t)
f(t)  M
so that by the properties of the Riemann integral we have that:
M
so that by the properties of the Riemann integral we have that:
But since f is continuous at x we know that m = M = f(x) as h goes to zero. Therefore: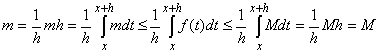
which proves the second assertion.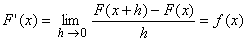
 Interactive Real Analysis
Interactive Real Analysis