7.1. Riemann Integral
Examples 7.1.4:
Suppose f(x) = x2 on [0, 2]. Find
The right and left Riemann sums are illustrated in the Java applet
below. To verify the result of that applet, let's perform the
computation manually as well.
- the fifth Riemann sum for an equally spaced partition, taking always the left endpoint of each subinterval
- the fifth Riemann sum for an equally spaced partition, taking always the right endpoint of each subinterval
- the n-th Riemann sum for an equally spaced partition, taking always the right endpoint of each subinterval.
The interval is [0, 2], and we want to find the fifth Riemann sum. Therefore the partition we need is:
x0 = 0, x1 = 2/5 = 0.4, x2 = 4/5 = 0.8,with a norm of | P | = 0.4. Taking the right points of each of the resulting intervals we can compute the right Riemann sum as:
x3 = 6/5 = 1.2, x4 = 8/5 = 1.6, x5 = 10/5 = 2
f(0.4)×0.4 + f(0.8)×0.4 + f(1.2)×0.4 + f(1.6)×0.4 + f(2)×0.4 =The left Riemann sum, correspondingly, computes to:
= 0.4×(f(0.4) + f(0.8) + f(1.2) + f(1.6) + f(2)) =
= 0.4×(0.42 + 0.82 + 1.22 + 1.62 + 22) =
= 0.4×(0.16 + 0.64 + 1.44 + 2.56 + 4) =
= 0.4×8.8 = 3.52
f(0.0)×0.4 + f(0.4)×0.4 + f(0.8)×0.4 + f(1.2)×0.4 + f(1.8)×0.4 =For the last part we can not use our Java applet since we do not have a numerical value for n. But we can manually compute the answer as follows: subdividing [0, 2] into n equal subintervals gives the partition:
= 0.4×(f(0.0) + f(0.4) + f(0.8) + f(1.2) + f(1.6)) =
= 0.4×(02 + 0.42 + 0.82 + 1.22 + 1.62) =
= 0.4×(0 + 0.16 + 0.64 + 1.44 + 2.56) =
= 0.4×4.8 = 1.92
xj = j×2/n, where j=0, 1, ... nTaking the right endpoint of all resulting subintervals and substituting them into the Riemann sum formula gives:
R(f, P) = f(2/n) × 2/n + f(4/n) × 2/n + ... + f( (n-1) 2/n ) + f(n 2/n)which works out to
R(f, P) = 2/n × ( (1 × 2/n)2 + (2 × 2/n)2 + ... + ( (n-1) × 2/n )2 + (n × 2/n)2)We can factor out 4/n2 to get:
R(f, P) = 8/n3 × (12 + 22 + ... + (n-1)2 + n2)In the chapter on induction we have shown that the sum of the first n square numbers equals
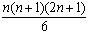 so that we
now have:
so that we
now have:
R(f, P) = 8/n3 ×We can substitute n = 5 to verify our formula:= 4/3 × (n+1) × (2n+1) / n2
R(f, Pn=5 ) = 4/3 ×6 ×11 / 25 = 88/25 = 3.52just as computed above.
 Interactive Real Analysis
Interactive Real Analysis