8.1. Pointwise Convergence
Example 8.1.7 (b): Pointwise Convergent Function Sequence
Show that
fn(x) = xn,
x  [ 0, 1 ]
[ 0, 1 ] converges
pointwise and identify the limit function.
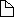
Back
|
Let 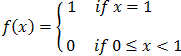
Then:
- if x = 1 we have fn(1) = 1 for all
n
- if x < 1 then fn(x) = xn
is the
power sequence and thus converges to zero
Hence fn(x) 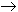 f(x)
for each fixed x. f(x)
for each fixed x.
|
|