3.5. Special Sequences
Definition 3.5.1: Power Sequence
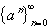 Power Sequence:
The convergence properties of the power sequence depends on the size of
the base a:
Power Sequence:
The convergence properties of the power sequence depends on the size of
the base a:
- |a| < 1: the sequence converges to 0.
- a = 1: the sequence converges to 1 (being constant)
- a > 1: the series diverges to plus infinity
- a
 -1: the series diverges
-1: the series diverges
Convergent Power series with a = -9/10
Divergent Power series with a = 11/10
Proof:
This seems an obvious statement: if a number is in absolute values less than one, it gets smaller and smaller when raised to higher and higher powers. Proving something 'obvious', however, is often difficult, because it may not be clear how to start. To prove the statement we have to resort to one of the elementary properties of the real number system: the Archimedian principle.- Case a > 1:
- Take any real number K > 0 and define
x = a - 1
Since a > 1 we know that x > 0. By the Archimedian principle there exists a positive integer n such that nx > K - 1. Using Bernoulli's inequality for that n we have:an = (1 + x)n
But since K was an arbitrary number, this proves that the sequence {an} is unbounded. Hence it can not converge. 1 + nx > 1 + (K - 1) = K
1 + nx > 1 + (K - 1) = K
- Case 0 < a < 1:
- Take any
 > 0.
Since 0 < a < 1 we know that 1/a > 1,
so that by the previous proof we can find an N with
> 0.
Since 0 < a < 1 we know that 1/a > 1,
so that by the previous proof we can find an N with
But then it follows that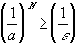
an <
This proves that the sequence {an} converges to zero. for all n > N
for all n > N
- Case -1 < a < 0:
- By the above proof we know that
| an | converges to zero. But since
-| an | < an < | an |
the sequence {an} again
converges to zero by the Pinching Theorem.
- Case a < -1:
- Extract the subsequence {a2m} from the
sequence {an}. Then this sequence diverges
to infinity by the first part of the proof, and therefore the original
sequence can not converge either.
- Case a = 1:
- This is the constant sequence, so it converges.
- Case a = -1:
- We have already proved that the sequence
j}.gif) does not converge.
does not converge.

 Interactive Real Analysis
Interactive Real Analysis