3.5. Special Sequences
Definition 3.5.3: Root of n Sequence
Root of n sequence
Proof:
If n > 1, then > 1. Therefore,
we can find numbers an > 0 such that
> 1. Therefore,
we can find numbers an > 0 such that
= 1 + an for each n > 1 Hence, we can raise both sides to the n-th power and use the Binomial theorem:
In particular, since all terms are positive, we obtain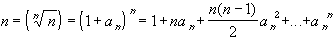 Solving this for an we obtain
Solving this for an we obtain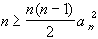 0But that implies that an converges to zero as n approaches to infinity, which means, by the definition of an that
0But that implies that an converges to zero as n approaches to infinity, which means, by the definition of an thatan

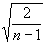
converges to 1 as n goes to infinity. That is what we wanted to prove.
 Interactive Real Analysis
Interactive Real Analysis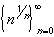 Root of n Sequence:
This sequence converges to 1.
Root of n Sequence:
This sequence converges to 1.
