3.5. Special Sequences
Definition 3.5.6: Euler Sequence
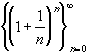 Euler's Sequence:
Converges to
e ~ 2.71828182845904523536028747135... (Euler's number). This
sequence serves to define e.
Euler's Sequence:
Converges to
e ~ 2.71828182845904523536028747135... (Euler's number). This
sequence serves to define e.
Euler's sequence
Proof:
We will show that the sequence is monotone increasing and bounded above. If that was true, then it must converge. Its limit, by definition, will be called e for Euler's number.Euler's number e is irrational (in fact transcendental), and an approximation of e to 30 decimals is e ~ 2.71828182845904523536028747135.
First, we can use the binomial theorem to expand the expression
Similarly, we can replace n by n+1 in this expression to obtain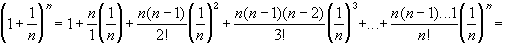
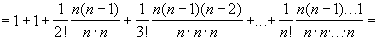
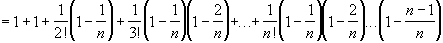
The first expression has (n+1) terms, the second expression has (n+2) terms. Each of the first (n+1) terms of the second expression is greater than or equal to each of the (n+1) terms of the first expression, because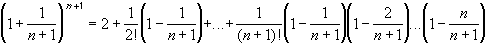
But then the sequence is monotone increasing, because we have shown that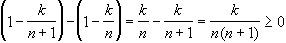
Next, we need to show that the sequence is bounded. Again, consider the expansion-
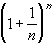
0
Now we need to estimate the expression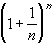
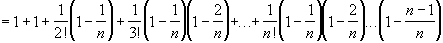

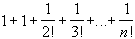
1 +
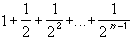
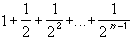 to finish the proof.
to finish the proof.
If we define
Sn = 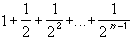 ,
then
,
then
so that, finally,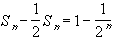
But then, putting everything together, we have shown thatfor all n.
for all n. Hence, Euler's sequence is bounded by 3 for all n.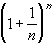
1 +
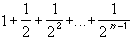
1 + Sn
3
Therefore, since the sequence is monotone increasing and bounded, it must converge. We already know that the limit is less than or equal to 3. In fact, the limit is approximately equal to 2.71828182845904523536028747135

 Interactive Real Analysis
Interactive Real Analysis