3.5. Special Sequences

Definition 3.5.5: Binomial Sequence

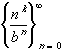Binomial Sequence: If b > 1 then the sequence converges to zero for any positive integer k. In fact, this is still true if k is replaced by any real number.

You browser is not 'Java-enabled' ...
Binomial sequence with k = 2 and b = 1.3

Proof:

Note that both numerator and denominator tend to infinity. Our goal will be to show that the denominator grows faster than the k-th power of n, thereby 'winning' the race to infinity and forcing the whole expression to tend to zero.

The name of this sequence indicates that we might try to use the binomial theorem for this. Indeed, define x such that

b = 1 + x
Since b > 1 we know that x > 0. Therefore, each term in the binomial theorem is positive, and we can use the (k+1)-st term of that theorem to estimate:
for any k+1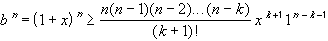 n. Let n = 2k + 1, or equivalently, k = (n-1)/2. Then n - k = n - (n-1)/2 = (n+1)/2 > n/2, so that each of the expressions n, n-1, n-2, ..., n - k is greater than n/2. Hence, we have that
But then, taking reciprocals, we have: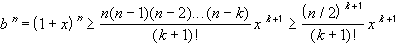
But this expression is true for all n > 2k + 1 as well, so that, with k fixed, we can take the limit as n approaches infinity and the right hand side will approach zero. Since the left-hand side is always greater than or equal to zero, the limit of the binomial sequence must also be zero.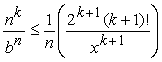

If k is replaced by any real number, see the exponential sequence to find out how nk could be defined for rational and irrational values of k. But perhaps some simple estimate will help if k is not an integer. Details are left as an exercise.

Next | Previous | Glossary | Map