3.1. Sequences
Proposition: Sup and Inf of bounded Sequences
If a sequence 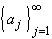 is
bounded above, then c = sup(aj) is finite.
Moreover, given any
is
bounded above, then c = sup(aj) is finite.
Moreover, given any
 > 0 there exists
at least one integer k such that
ak > c -
> 0 there exists
at least one integer k such that
ak > c -  (see picture).
(see picture).
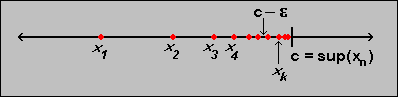
If a sequence 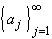 is
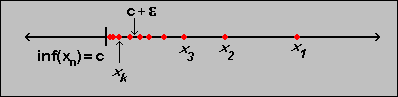
bounded below, then
c = inf(aj) is finite. Moreover, given any
is
bounded below, then
c = inf(aj) is finite. Moreover, given any
 > 0, there exists
at least one integer k such that
ak < c +
> 0, there exists
at least one integer k such that
ak < c +  (see picture).
(see picture).
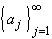 is
bounded above, then c = sup(aj) is finite.
Moreover, given any
is
bounded above, then c = sup(aj) is finite.
Moreover, given any
 > 0 there exists
at least one integer k such that
ak > c -
> 0 there exists
at least one integer k such that
ak > c -  (see picture).
(see picture).

 is
bounded below, then
c = inf(aj) is finite. Moreover, given any
is
bounded below, then
c = inf(aj) is finite. Moreover, given any
 > 0, there exists
at least one integer k such that
ak < c +
> 0, there exists
at least one integer k such that
ak < c +  (see picture).
(see picture).

Proof:
We will only prove the first statement, leaving the second one involving inf as an exercise.Recall that the sup is the smallest of all upper bounds. Since the sequence is assumed to be bounded above, the sup must be less than or equal to that upper bound, by definition. Therefore the sup can not be positive infinity. But the sup must also be at least as big as the first number of the sequence, hence the sup can not be negative infinity. Therefore, the sup must be bounded.
The second statement can be proved by contradiction, which means that we first need to figure out the contra-positive of the statement to be proved (which is the only hard part of the proof). We need to turn every "take any" to "there exists", any "at least one" to "for all", and switch the inequality.
But that opposite statement implies immediately that c -
- Original statement:
- Suppose that c = sup(aj). Then given any
> 0 there exists at least one integer k such that ak > c -

- Opposite of that statement:
- Suppose that c = sup(aj). Then there exists one
> 0 such that for all integers k we have ak < c -

 would be a new upper bound for the sequence {aj},
and clearly c -
would be a new upper bound for the sequence {aj},
and clearly c -  < c.
But then c could not have been the original sup
of the sequence, because the must be the smallest one of all upper
bounds. Therefore we have our contradiction and the original statement
is proved.
< c.
But then c could not have been the original sup
of the sequence, because the must be the smallest one of all upper
bounds. Therefore we have our contradiction and the original statement
is proved.
 Interactive Real Analysis
Interactive Real Analysis