3.1. Sequences

Theorem 3.1.11: The Pinching Theorem

Suppose {aj} and {cj} are two convergent sequences such that lim aj = lim cj = L. If a sequence {bj} has the property that
aj bj cj
for all j, then the sequence {bj} converges and lim bj = L.

Proof:

The statement of the theorem is easiest to memorize by looking at a diagram: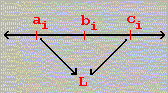
All bj are between aj and cj, and since aj and cj converge to the same limit L the bj have no choice but to also converge to L.

Of course this is not a formal proof, so here we go: we want to show that given any > 0 there exists an integer N such that | bj - L | < if j > N. We know that

aj bj cj
Subtracting L from these inequalities gives:
aj - L bj - L cj - L
But there exists an integer N1 such that | aj - L | < or equivalently
- < aj - L <
and another integer N2 such that | cj - L | < or equivalently
- < cj - L <
if j > max(N1, N2). Taking these inequalities together we get:
- < aj - L bj - L cj - L <
But that means that
- < bj - L <
or equivalently | bj - L | < as long as j > max(N1, N2). But that means that {bj} converges to L, as required.

Next | Previous | Glossary | Map