3.1. Sequences
Proposition 3.1.6: Algebra on Convergent Sequences
Suppose  and
and
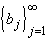 are converging
to a and b, respectively. Then
are converging
to a and b, respectively. Then
 and
and
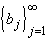 are converging
to a and b, respectively. Then
are converging
to a and b, respectively. Then
- Their sum is convergent to a + b, and the sequences can be added term by term.
- Their product is convergent to a * b, and the sequences can be multiplied term by term.
- Their quotient is convergent to a / b, provide that b # 0, and the sequences can be divided term by term (if the denominators are not zero).
- If an
 bn
for all n, then a
bn
for all n, then a  b
b
Proof:
The proofs of these statements involve the triangle inequality, as well as an occasional trick of adding and subtracting zero, in a suitable form. A proof of the first statement, for example, goes as follows.
Take any  > 0. We know that
an
> 0. We know that
an 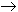 a, which
implies that there exists an integer N1 such that
a, which
implies that there exists an integer N1 such that
| an - a | <if n > N1. Similarly, since bn/ 2
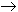 b
there exists another integer N2 such that
b
there exists another integer N2 such that
| bn - b | <if n > N2. But then we know that/ 2
| (an + bn) - (a + b) | = | (an - a) + (bn - b) |if n > max(N1, N2), which proves the first statement.
| an - a | + | bn - b |
</2 +
/2 =

Proving the second statement is similar, with some added tricks. We know that { bn } converges, therefore there exists an integer N1 such that
| bn | < |b| + 1if n > N1. We also know that we can find integers N2 and N3 so that
| an - a | <if n > N2, and/ (|b| + 1)
| bn - b | <if n > N3, because |a| and |b| are some fixed numbers. But then we have:/ (|a| + 1)
| an bn - a b | = | an bn - a bn + a bn - a b |if n > max(N1, N2, N3), which proves the second statement.
= | bn(an - a) + a (bn - b) |
| bn| |an - a | + | a | | bn - b |
< (| b | + 1)/ (|b| + 1) + | a |
/ (|a| +1) < 2

The proof of the third statement is similar, so we will leave it as an exercise.
The last statement does require a new trick: we will use a proof by contradiction to get that result:
Assume that anWe now need to work out the contradiction: the idea is that since a > b there is some number c such that b < c < a.bn for all n, but a > b.
Since an converges to a, we can make the terms of the sequence fall between c and a, and the terms of bn between b and c. But then we no longer have that an<----------[b]-------[a]--------> <----------[b]--[c]--[a]-------->
 bn,
which is our contradiction. Now let's formalize this idea:
bn,
which is our contradiction. Now let's formalize this idea:
Let c = (a + b)/2. Then clearly b < c < a (verify!). Choose N1 such that bn < c if n > N1. That works because b < c. Also choose N2 such that an > c if n > N2. But now we have that
bn < c < anfor n > max(N1, N2). That is a contradiction to the original assumption that an
 bn for
all n. Hence it can not be true that a > b, so that
the statement is indeed proved.
bn for
all n. Hence it can not be true that a > b, so that
the statement is indeed proved.

 Interactive Real Analysis
Interactive Real Analysis