Interactive Real Analysis

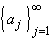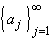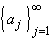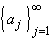Let be a sequence of real numbers. Define

A_j = inf{ a_j , a_{j + 1} , a_{j + 2} , ...}

and let c = lim (A_j). Then c is called the limit inferior of the sequence .

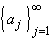Let 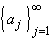be a sequence of real numbers. Define

B_j = sup{ a_j , a_{j + 1} , a_{j + 2} , ...}

and let c = lim (B_j). Then c is called the limit superior of the sequence .

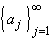In short, we have:

1. lim inf(a_j) = lim(A_j), where A_j = inf{a_j , a_{j + 1} , a_{j + 2} , ...}
2. lim sup(a_j) = lim(B_j), where B_j = sup{ a_j , a_{j + 1} , a_{j + 2} , ...}