3.1. Sequences
Examples 3.1.8(a):
One can start to investigate this statement without having to suspect the correct answer. We will simply compare the quotient of two consecutive terms to check whether the answer is greater or less than one:(1/n) / (1/ (n+1) ) = (n+1) / n > 1Hence, the n-th term of the sequence divided by the (n+1) term is always greater than 1, or, in other words, the n-th term is greater than the (n+1)-th term.
That is the definition of a decreasing sequence so that the sequence is decreasing. Checking a graphical representation of this sequence confirms that.
 Interactive Real Analysis
Interactive Real Analysis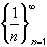 monotone increasing or decreasing ?
monotone increasing or decreasing ?