3.1. Sequences
Examples 3.1.10(a):
First, let us consider the sequence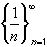 .
It is decreasing because:
.
It is decreasing because:
( 1/n ) - (1 / (n+1) ) > 0Also, the sequence is bounded below by 0, because each term is positive. Hence, the sequence must converge.
Note that this does not tell us the actual limit. But we have proved before that this sequence converges to 0.
Next, we consider the sequence
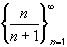 .
This sequence is increasing because
.
This sequence is increasing because
n / (n+1) - (n+1) / (n + 2) < 0The sequence is also bounded above by 1, because n < n + 1 so that
n / (n + 1) < 1Hence, the sequence must converge.
Note that this does not tell us what the limit of the sequence is. However, the limit is equal to 1, as you can easily prove yourself.
 Interactive Real Analysis
Interactive Real Analysis