1. Sets and Relations
1.3. Equivalence Relations and Classes
Just as there were different classes of functions (bijections, injections, and surjections),
there are also special classes of relations. One of the most useful kind of relation (besides
functions, which of course are also relations) are those called equivalence relations.
| Definition 1.3.1: Equivalence Relation |
| |
Let S be a set and r a relation between S and itself. We call r an
equivalence relation on S if r has the following three properties:
- Reflexivity: Every element of S is related to itself
- Symmetry: If s is related to t then t
is related to s
- Transitivity: If s is related to t and t
is related to u, then s is related to u.
|
| Examples 1.3.2: |
| |
- Let A = {1, 2, 3, 4} and B = {a, b, c} and define the following
two relations:
- r : { (a,a), (b,b), (a,b), (b,a) }
- s : 1 ~ 1, 2 ~ 2, 3 ~ 3, 4 ~ 4, 1 ~ 4, 4 ~ 1, 2 ~ 4, 4 ~ 2
 Which one is an equivalence relation, if any ?
Which one is an equivalence relation, if any ?
|
At first glance equivalence relations seem to be too abstract to be useful. However, just
the opposite is the case. Because they are defined in an abstract fashion, equivalent
relations can be utilized in many different situations. In fact, they can be used to define
such basic objects as the integers, the rational numbers, and the real numbers.
The main result about an equivalence relation on a set A is that it induces a
partition of A into disjoint sets. This property is the one that will allow us to
define new mathematical objects based on old ones in the next section.
| Example 1.3.4: |
| |
 Consider the set Z of all integers. Define a relation r by
saying that x and y are related if their difference
y - x is divisible by 2. Then
Consider the set Z of all integers. Define a relation r by
saying that x and y are related if their difference
y - x is divisible by 2. Then
- Check that this relation is an equivalence relation
- Find the two equivalence classes, and name them appropriately.
- How would you add these equivalence classes, if at all ?
 What kind of equivalence classes do you get when x and y are
defined to be related if their difference is divisible by m ? How could
you add those ?
What kind of equivalence classes do you get when x and y are
defined to be related if their difference is divisible by m ? How could
you add those ?
|
Here is another, more complicated example:
| Example 1.3.5: |
| |
- Consider the set R x R \ {(0,0)} of all points in the plane minus
the origin. Define a relation between two points (x,y) and
(x', y') by saying that they are related if they are lying on the same
straight line passing through the origin. Then:
 Check that this relation is an equivalence relation and find a graphical
representation of all equivalence classes by picking an appropriate member for each class.
Check that this relation is an equivalence relation and find a graphical
representation of all equivalence classes by picking an appropriate member for each class.
- The space of all equivalence classes obtained under this equivalence relation is called
projective space.
|
More examples for equivalence relations and their resulting classes are given in the next
section.
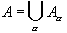 with the
following properties:
with the
following properties:
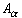 are called
equivalence classes.
are called
equivalence classes.
 Interactive Real Analysis
Interactive Real Analysis