1.3. Equivalence Relations and Classes
Example 1.3.5:
This relation is an equivalence relation, and the resulting space of equivalence classes is called projective space. By picking an appropriate member for each class one can find a graphical representation for this space.
- reflexive:
- every point is related to itself, since it lies on a line through the origin.
- symmetry:
- if (x, y) ~ (x', y'), then they are both on the same line through the origin. This is a symmetric definition, so symmetry holds as well.
- transitivity:
- here we should use some math. Recall that two points (x, y) and
(x', y') are on the same line through the origin, if and only if
there is a non-zero real number t such that (x, y) = t (x', y').
- take (x, y) ~ (x', y').
- take (x', y') ~ (x'', y'')
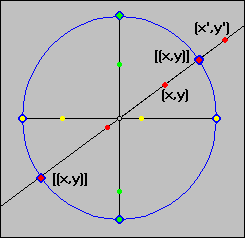
Since the relation is an equivalence relation we know that there are disjoint equivalence classes [(x, y)], and we can pick any member of [(x, y)] as a representative of that class. Define a point p on the unit circle to be equal to the whole equivalence class [(x, y)] containing p. That is, we identify each equivalence class with a point on the unit circle by drawing the line through that point and the origin. That line contains every member of the equivalence class.
Numbers on the unit circle that are diagonally opposite each other, however, are in the same equivalence class, since they are on the same line through the origin.Thus we identify the space P with the unit circle, where diagonally opposite numbers are identical. Here is a poor picture of this space:
 Interactive Real Analysis
Interactive Real Analysis