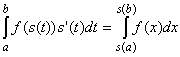7.2. Integration Techniques
Theorem 7.2.3: Substitution Rule
If f is a continuous function defined on [a, b], and
s a continuously differentiable function from [c, d] into
[a, b]. Then
Proof:
f is continuous so that there exists a function F with F' = f (in other words, F is an antiderivative of f). Differentiate the function F(s(x)) using the Chain Rule:because F' = f. Therefore the composite function F(s(x)) is an antiderivative of f(s(x)) s'(x) so that by our evaluation shortcut we have:F(s(x)) = F'(s(x)) s'(x) = f(s(x)) s'(x)
But since F is by assumption an antiderivative of f we have thatf(s(t)) s'(t) dt = F(s(b)) - F(s(b))
which finishes the proof.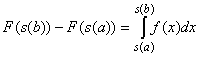
 Interactive Real Analysis
Interactive Real Analysis