7.1. Riemann Integral
Theorem 7.1.14: Riemann Integrals of Continuous Functions
Proof:
We have shown before that f(x) = x2 is integrable where we used the fact that f was differentiable. We will now adjust that proof to this situation, using uniform continuity instead of differentiability. We can actually simplify the previous proof because we now have Riemann's lemma at our disposal.
We know that f is continuous over a closed and bounded interval.
Therefore f must be uniformly continuous over [a, b], i.e.
for any given  > 0
we can find a
> 0
we can find a  > 0
such that
|f(x) - f(y)| <
> 0
such that
|f(x) - f(y)| <  for all x and y with
|x - y| <
for all x and y with
|x - y| <  .
.
Now take any  > 0 and
choose a partition P with
|P| <
> 0 and
choose a partition P with
|P| <  . Then
. Then
| U(f, P) - L(f, P)|where cj is the sup of f over [xj-1, xj] and dj is the inf over that interval. Since the function is continuous, it assumes its maximum and minimum over each of the subintervals, so that inf and sup can be replaced with min and max.
|cj - dj| (xj - xj-1)
Since the norm of the partition is less than
 we know that
|cj - dj| <
we know that
|cj - dj| <  for all j.
for all j.
But then
| U(f, P) - L(f, P)|because the last sum is telescoping. That finishes the proof.

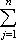
(xj - xj-1)
=
(xj - xj-1)
=(xn - x0)
=(b - a)
For the purist, we should have chosen  such that |f(x) - f(y)| <
such that |f(x) - f(y)| <  / (b-a) whenever
|x - y| <
/ (b-a) whenever
|x - y| <  so that at the end of our
above computation we could get a single
so that at the end of our
above computation we could get a single  .
But that's just details...
.
But that's just details...
It is easy to find an example of a function that is Riemann integrable but not continuous. For example, the function f that is equal to -1 over the interval [0, 1] and +1 over the interval [1, 2] is not continuous but Riemann integrable (show it!).

 Interactive Real Analysis
Interactive Real Analysis