7.4. Lebesgue Integral
Definition 7.4.13: Measurable Function
Let f be a function from
E  R
into
R
R
into
R 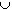 { -
{ -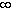 ,
, 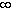 }
. The function f is called (Lebesgue) measurable if
}
. The function f is called (Lebesgue) measurable if
 R
into
R
R
into
R 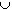 { -
{ -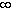 ,
, 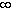 }
. The function f is called (Lebesgue) measurable if
}
. The function f is called (Lebesgue) measurable if
- the domain E of the function is a measurable set
- for every real number a the set
f -1 (-
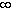 , a)
is a measurable set
, a)
is a measurable set
 Interactive Real Analysis
Interactive Real Analysis