7.1. Riemann Integral
Examples 7.1.6(b):
Why is, in general, an upper (or lower) sum not a special case of
a Riemann sum ? Find a condition for a function f so
that the upper and lower sums are actually special cases of
Riemann sums.
The reason is simple: a Riemann sum requires points where the function
is defined, while an upper/lower sum involves an sup/inf which may not
correspond to points in the range of the function.
What this means is best illustrated via an example. Take the function
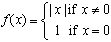 |
|
So to find a condition that ensures that upper/lower sums are special cases of Riemann sums we must ensure that the sup/inf that appears in the definition of upper/lower sum is a max or min, respectively. In the topology chapter we have shown that a continuous function over a closed, bounded interval must have a max and a min.
Therefore, if f is continuous over the interval [a, b] then the upper and the lower sum are both special cases of a Riemann sum.
 Interactive Real Analysis
Interactive Real Analysis