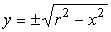7.2. Integration Techniques
Example 7.2.4(c): Applying the Substitution Rule
Of course everyone knows that the correct answer is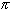 r2,
but we want to compute the answer, not just state it.
r2,
but we want to compute the answer, not just state it.
First we need to describe the circle mathematically. We know that
x2 + y2 = r2 is a circle,
which we can solve for y:
where the positive root gives the upper half-circle (blue) and the negative one the lower part (red). |
Now we need to guess a change of variables that will make this integrand easier. Since we are dealing with a circle, the trig functions sin and cos might come to mind, and especially the fact that sin(t)2 + cos(t)2 = 1, or equivalently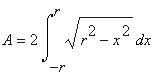
r2 - (r cos(t))2 = (r sin(t))2Therefore we try the following substitution:
x = r sin(t) so thatWith that substitution the integral is transformed into a much simpler version:
dx/dt = r cos(t) or dx = r cos(t) dt
where we determine the new integration interval [a, b] later. Now we need to remember a few facts about trig functions, in particular the so-called "double-angle" formula: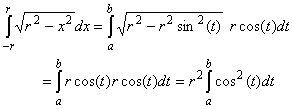
cos2(t) = 1/2 (cos(2t) + 1)Therefore our area is
A = 2 r2/2where we have used the substitution u = 2t in our head to evaluate the first integral.cos(2t) + 1 dt = r2 [
cos(2t) dt +
1 dt ] =
= r2 [1/2 ( sin(2b) - sin(2a) ) + (b - a)]
It remains to find the values of a and b. They originate from the original substitution of x = r sin(t). Therefore x = -r must correspond to a such that r sin(a) = -r and x = r must correspond to b where r sin(b) = r:
-r = r sin(a) and r = r sin(b)Therefore a = -
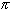 /2 and
b =
/2 and
b = 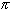 /2. Now we can compute the
final answer:
/2. Now we can compute the
final answer:
A = r2 [1/2 ( sin(2b) - sin(2a) ) + (b - a)] =Lucky us, we got the correct answer! Note that this time our change of variables is different from our previous examples:
= r2 [1/2 ( sin() - sin(-
) +
] =
=r2
But as long as we correctly transform the dx term based on our substitution, anything goes.
- usually we change an expression in x to a single variable u.
- this time we changed a single variable x to an expression in another variable t.
 Interactive Real Analysis
Interactive Real Analysis