7.2. Integration Techniques

Example 7.2.4(b): Applying the Substitution Rule

If F(x) is an antiderivative of f(x), find:
  • f(cx + d) dx
  • x f(cx2) dx
  • f'(x) / f(x) dx
To find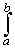 f(cx + d) dx we make the substitution
u = cx + d so that
du/dx = c, or du = c dx
Therefore
f(cx + d) dx = f(u) dx =
      = 1/c f(u) c dx = 1/c f(u) du =
      = 1/c [F(u(b)) - F(u(a))] = 1/c [F(cb + d) - F(ca + d)]
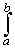To find x f(cx2) dx we make the substitution
u = cx2 so that
du/dx = 2cx or du = 2cx dx
Therefore
x f(cx2) dx = x f(u) dx =
      = 1/2c f(u) 2cx dx = 1/2c f(u) du =
      = 1/2c [ F(u(b)) - F(u(a)) ] = = 1/2c [ F(cb2) - F(ca2) ]
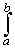To find f'(x) / f(x) dx we make the substitution
u = f(x) so that
du/dx = f'(x), or du = f'(x) dx
Therefore
f'(x) / f(x) dx = 1/ f(x) f'(x) dx = 1/u du =
      = ln(|f(b)|) - ln(|f(a)|)
Next | Previous | Glossary | Map