7.2. Integration Techniques
Example 7.2.4(a): Applying the Substitution Rule
Here is a simple example: find
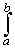 (4x + 3)2 dx
(4x + 3)2 dx.
Back
The expression that makes the integral difficult is
4x + 3 so
that we make the change of variable
u = 4x + 3
Then
du/dx = 4, or du = 4 dx
which at first glance does not appear in the original integral. But:
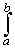 (4x + 3)2 dx =
(4x + 3)2 dx =
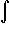 u2 1/4 4 dx =
u2 1/4 4 dx =
= 1/4 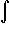 u2 4 dx =
1/4
u2 4 dx =
1/4 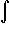 u2 du =
u2 du =
= 1/4 1/3 [(4b + 3)3 - (4a + 3)3]
There is no "incorrect" substitution, you can make any change of variables that
you want. There
are, however, substitutions that work (such as above) and those
that do not work (which are not incorrect but not successful). For
example, we could decide to make the following substitution in the above example:
u = (4x + 3)2
Then
du/dx = 2 (4x + 3) 4 or du = 8 (4x + 3) dx
The new integral looks like
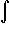 u dx
u dx,
but it is not (easily) possible to remove the
dx. Therefore, this substitution,
while correct, was not successful.
(4x + 3)2 dx =
u2 1/4 4 dx =
u2 4 dx = 1/4
u2 du =
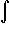 u dx,
but it is not (easily) possible to remove the dx. Therefore, this substitution,
while correct, was not successful.
u dx,
but it is not (easily) possible to remove the dx. Therefore, this substitution,
while correct, was not successful.
 Interactive Real Analysis
Interactive Real Analysis