7.2. Integration Techniques

Example 7.2.6(c): Applying Integration by Parts

Find 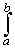ln(x) dx
Integration by parts seems not applicable here because there is no product. But we can trivially write the integrand as 1 ln(x). Then we define the functions
  • g'(x) = 1 so that g(x) = x
  • f(x) = ln(x) so that f'(x) = 1/x
With G(x) = x ln(x) we have
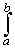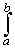ln(x) dx = G(b) - G(a) - x 1/x dx =
      = b ln(b) - a ln(a) - (b - a)
The trick here was to realize that integration by parts could be used at all, not the actual mechanics of the process.
Next | Previous | Glossary | Map