7.1. Riemann Integral
Examples 7.1.21(b):
Find the value of the following integrals:
This time we will use the Integral Evaluation Shortcut, or First
Fundamental Theorem of Calculus, which requires us to find the
antiderivative for each of the functions.
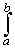 x5 - 4 x2 dx
on the interval [0, 2].
x5 - 4 x2 dx
on the interval [0, 2].
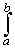 1/x2 + cos(x) dx
on the interval [1, 4].
1/x2 + cos(x) dx
on the interval [1, 4].
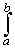 (1 + x2)-1 dx
on the interval [-1, 1].
(1 + x2)-1 dx
on the interval [-1, 1].
1.
Here is a numerical approximation of
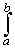 x5 - 4 x2 dx
on the interval [0, 2].
x5 - 4 x2 dx
on the interval [0, 2].
P(x) = 1/6 x6 - 4/3 x3 + CThen we clearly have:
P'(x) = x5 - 4 x2so that P is an antiderivate of the integrand. Therefore:
With our choices of a and b we can evaluate the integral tox5 - 4 x2 dx = P(b) - P(a)
P(2) - P(0) = 1/6 26 - 4/3 23 = 1/6 64 - 4/3 * 8 = 0
2.
Here is a numerical approximation of
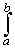 1/x2 + cos(x) dx
on the interval [1, 4].
1/x2 + cos(x) dx
on the interval [1, 4].
P(4) - P(1) = -1/4 + sin(4) - (-1/1 + sin(1)) = -.8482734801
3.
Here is a numerical approximation of
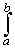 (1 + x2)-1 dx
on the interval [-1, 1].
(1 + x2)-1 dx
on the interval [-1, 1].
But then the integral evaluates toarctan(x) = (1 + x2)-1
arctan(1) - arctan(-1) = 2/4 =
/2 = 1.570796327
 Interactive Real Analysis
Interactive Real Analysis